STAT 330 Lecture 21

Reading for Today's Lecture: 10.1.

Goals of Today's Lecture:

• Learn more about the geometry of an ANOVA table.
• Learn what a model equation is.
• Learn that least squares and maximum likelihood methods are the same for normal populations.

Today's notes

Geometry

Write the data, out as a big vector

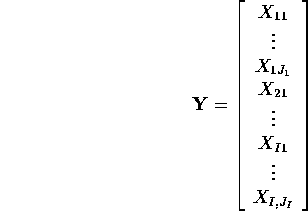
Now we write

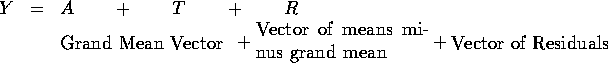
Writing the equation for a particular component of this vector we have

Here are the Geometric facts:

1. Y, A, T, and R are vectors in Euclidean space of dimensions.
2. A, T and R are all perpendicular.
3. The ANOVA identity is

   

   The squared lengths of these 4 vectors are called the Total Sum of squares ( ), the Sum of Squares due to the Grand Mean ( ), the Sum of Squares due to Treatment ( ) and the Sum of Squares due to Error ( ).

4. Usually we move the grand mean to the other side and write

   

   and

   

   The quantity is called the Corrected Total Sum of Squares.

Here is a proof that A and T are perpendicular. The proofs are similar for and .

Recall that if

and

then x and y are perpendicular ( ) if

Then

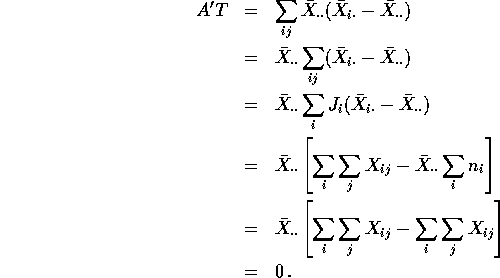
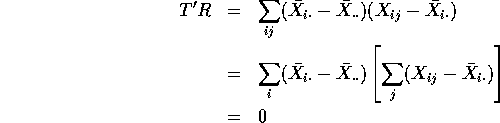
because . The sum of deviations from average in any list is 0. This shows .

Model equations

For this section we take all -- all sample sizes equal.

Our model is

which we can rewrite as

If we define which we call the underlying, or true, residuals and we define the population Grand Mean by

and we can write

We call this equation a Model Equation. The three pieces of the right hand side of this equation correspond to three pieces on the right hand side of our decomposition of the data

and we have

This identities for the equal sample size case motivate the general definition for unequal sample sizes

and

It is automatically true that

Least squares

Write our model as

where the errors are iid . If we stack up our data in the vector Y as

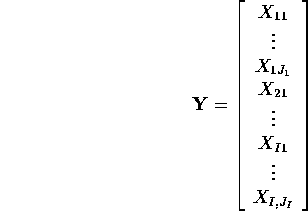
then the method of least squares consists of estimating , by finding the vector of the form

which is closest to the data vector Y. We measure distance in the usual Euclidean distance way. The solution is to find the orthogonal projection of Y onto the space of vectors of the form

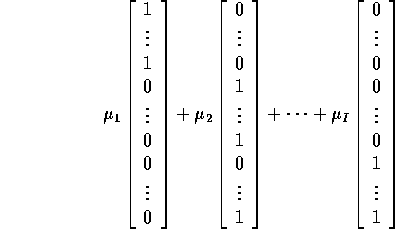
It is then automatic that the projection of Y is perpendicular to Y minus the projection of Y.

How do we compute this projection? We find the vector

closest to Y by minimizing the squared distance from this vector to Y. This squared distance is just

To minimize this we set the partial derivatives with respect to each equal to 0 for . We get

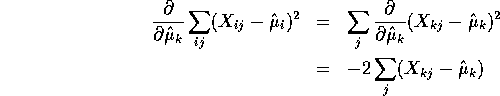
which is equal to 0 if and only if

This method is called least squares.

Remark: This method shows that A+T (which is the projection of Y) is perpendicular to R (which is Y-(A+T) by definition).

Null hypothesis Case

If is true then the model equation is

If the errors were 0 then the vector Y would simply be

We find the vector of the form

closest to Y. Again we project Y onto the subspace of vectors spanned by

by minimizing the squared distance which is

This is minimized by

Least squares and maximum likelihood

The likelihood function is

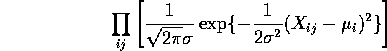
If we assume that the null hypothesis is true then the likelihood simplifies to

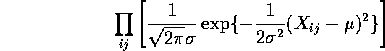
The log likelihood is

or in the null hypothesis case

To find the MLE of the parameters and we must maximize these log likelihood functions. But notice that the 's occur only in the sums of squares which are multiplied by a negative sign. For any value of we can choose the 's to maximize the log likelihood by minimizing the sum of squares. This means:

Least squares is the same as maximum likelihood for normally distributed errors -- at least in terms of estimating means.

What do you do after testing ?

In our coagulation example we concluded that all the mean coagulation times were not the same. What next?

1: Model diagnostics

• examine residual plots such as residual versus treatment group or residual versus group mean.
• examine a histogram of dot-plot of residuals
• make a Q-Q plot of the residuals

1: Confidence Intervals

• for either
  • ``one at a time'' or
  • ``simultaneous''

• for general contrasts like