TRANSFORM Statement

The PRINQUAL Procedure

TRANSFORM Statement

TRANSFORM transform(variables < / t-options >)

< ... transform(variables < / t-options >) > ;

The TRANSFORM statement lists the variables to be analyzed (variables) and specifies the transformation (transform) to apply to each variable listed. You must specify a transformation for each variable list in the TRANSFORM statement. The variables are variables in the data set. The t-options are transformation options that provide details for the transformation; these depend on the transform chosen. The t-options are listed after a slash in the parentheses that enclose the variables.

For example, the following statements find a quadratic polynomial transformation of all variables in the data set:

   proc prinqual;
      transform spline(_all_ / degree=2);
   run;

Or, if N1 through N10 are nominal variables and M1 through M10 are ordinal variables, you can use the following statements.

   proc prinqual;
      transform opscore(N1-N10) monotone(M1-M10);
   run;

The following sections describe the transformations available (specified with transform) and the options available for some of the transformations (specified with t-options).

Families of Transformations

There are three types of transformation families: nonoptimal, optimal, and other. Each family is summarized as follows.

Nonoptimal transformations: preprocess the specified variables, replacing each one with a single new nonoptimal, nonlinear transformation.
Optimal transformations: replace the specified variables with new, iteratively derived optimal transformation variables that fit the specified model better than the original variable (except for contrived cases where the transformation fits the model exactly as well as the original variable).
Other transformations: are the IDENTITY and SSPLINE transformations. These do not fit into either of the preceding categories.

The following table summarizes the transformations in each family.

	Members
Family	of Family
Nonoptimal transformations
inverse trigonometric sine	ARSIN
exponential	EXP
logarithm	LOG
logit	LOGIT
raises variables to specified power	POWER
transforms to ranks	RANK
Optimal transformations
linear	LINEAR
monotonic, ties preserved	MONOTONE
monotonic B-spline	MSPLINE
optimal scoring	OPSCORE
B-spline	SPLINE
monotonic, ties not preserved	UNTIE
Other transformations
identity, no transformation	IDENTITY
iterative smoothing spline	SSPLINE

The transform is followed by a variable (or list of variables) enclosed in parentheses. Optionally, depending on the transform, the parentheses can also contain t-options, which follow the variables and a slash. For example,

   transform log(X Y);

computes the LOG transformation of X and Y. A more complex example is

   transform spline(Y / nknots=2) log(X1 X2 X3);

The preceding statement uses the SPLINE transformation of the variable Y and the LOG transformation of the variables X1, X2, and X3. In addition, it uses the NKNOTS= option with the SPLINE transformation and specifies two knots.

The rest of this section provides syntax details for members of the three families of transformations. The t-options are discussed in the section "Transformation Options (t-options)".

Nonoptimal Transformations

Nonoptimal transformations are computed before the iterative algorithm begins. Nonoptimal transformations create a single new transformed variable that replaces the original variable. The new variable is not transformed by the subsequent iterative algorithms (except for a possible linear transformation and missing value estimation).

The following list provides syntax and details for nonoptimal variable transformations.

ARSIN

ARS

finds an inverse trigonometric sine transformation. Variables following ARSIN must be numeric, in the interval $(-1.0 \leq {{\hv X}} \leq 1.0)$ , and they are typically continuous.

EXP

exponentiates variables (the variable X is transformed to a^X). To specify the value of a, use the PARAMETER= t-option. By default, a is the mathematical constant e = 2.718 .... Variables following EXP must be numeric, and they are typically continuous.

LOG

transforms variables to logarithms (the variable X is transformed to log_a(X)). To specify the base of the logarithm, use the PARAMETER= t-option. The default is a natural logarithm with base e = 2.718 .... Variables following LOG must be numeric and positive, and they are typically continuous.

LOGIT

finds a logit transformation on the variables. The logit of X is log(X/(1-X)). Unlike other transformations, LOGIT does not have a three-letter abbreviation. Variables following LOGIT must be numeric, in the interval (0.0 < X < 1.0), and they are typically continuous.

POWER

POW

raises variables to a specified power (the variable X is transformed to X^a). You must specify the power parameter a by specifying the PARAMETER= t-option following the variables:

   power(variable / parameter=number)

You can use POWER for squaring variables (PARAMETER=2), reciprocal transformations (PARAMETER=-1), square roots (PARAMETER=0.5), and so on. Variables following POWER must be numeric, and they are typically continuous.

RANK

RAN

transforms variables to ranks. Ranks are averaged within ties. The smallest input value is assigned the smallest rank. Variables following RANK must be numeric.

Optimal Transformations

Optimal transformations are iteratively derived. Missing values for these types of variables can be optimally estimated (see the "Missing Values" section).

The following list provides syntax and details for optimal transformations.

LINEAR
LIN: finds an optimal linear transformation of each variable. For variables with no missing values, the transformed variable is the same as the original variable. For variables with missing values, the transformed nonmissing values have a different scale and origin than the original values. Variables following LINEAR must be numeric.
MONOTONE
MON: finds a monotonic transformation of each variable, with the restriction that ties are preserved. The Kruskal (1964) secondary least-squares monotonic transformation is used. This transformation weakly preserves order and category membership (ties). Variables following MONOTONE must be numeric, and they are typically discrete.
MSPLINE
MSP: finds a monotonically increasing B-spline transformation with monotonic coefficients (de Boor 1978; de Leeuw 1986) of each variable. You can specify the DEGREE=, KNOTS=, NKNOTS=, and EVENLY t-options with MSPLINE. By default, PROC PRINQUAL uses a quadratic spline. Variables following MSPLINE must be numeric, and they are typically continuous.
OPSCORE
OPS: finds an optimal scoring of each variable. The OPSCORE transformation assigns scores to each class (level) of the variable. Fisher's (1938) optimal scoring method is used. Variables following OPSCORE can be either character or numeric; numeric variables should be discrete.
SPLINE
SPL: finds a B-spline transformation (de Boor 1978) of each variable. By default, PROC PRINQUAL uses a cubic polynomial transformation. You can specify the DEGREE=, KNOTS=, NKNOTS=, and EVENLY t-options with SPLINE. Variables following SPLINE must be numeric, and they are typically continuous.
UNTIE
UNT: finds a monotonic transformation of each variable without the restriction that ties are preserved. The PRINQUAL procedure uses the Kruskal (1964) primary least-squares monotonic transformation method. This transformation weakly preserves order but not category membership (it may untie some previously tied values). Variables following UNTIE must be numeric, and they are typically discrete.

Other Transformations

IDENTITY
IDE: specifies variables that are not changed by the iterations. The IDENTITY transformation is used for variables when no transformation and no missing data estimation are desired. However, the REFLECT, ADDITIVE, TSTANDARD=Z, and TSTANDARD=CENTER options can linearly transform all variables, including IDENTITY variables, after the iterations. Observations with missing values in IDENTITY variables are excluded from the analysis, and no optimal scores are computed for missing values in IDENTITY variables. Variables following IDENTITY must be numeric.
SSPLINE
SSP: finds an iterative smoothing spline transformation of each variable. The SSPLINE transformation does not generally minimize squared error. You can specify the smoothing parameter with either the SM= t-option or the PARAMETER= t-option. The default smoothing parameter is SM=0. Variables following SSPLINE must be numeric, and they are typically continuous.

Transformation Options (t-options)

If you use a nonoptimal, optimal or other transformation, you can use t-options, which specify additional details of the transformation. The t-options are specified within the parentheses that enclose variables and are listed after a slash. For example,

   proc prinqual;
      transform spline(X Y / nknots=3);
   run;

The preceding statements find an optimal variable transformation (SPLINE) of the variables X and Y and use a t-option to specify the number of knots (NKNOTS=). The following is a more complex example.

   proc prinqual;
      transform spline(Y / nknots=3) spline(X1 X2 / nknots=6);
   run;

These statements use the SPLINE transformation for all three variables and use t-options as well; the NKNOTS= option specifies the number of knots for the spline.

The following sections discuss the t-options available for nonoptimal, optimal, and other transformations.

The following table summarizes the t-options.

Table 53.1: t-options Available in the TRANSFORM Statement

Task	Option
Nonoptimal transformation t-options
uses original mean and variance	ORIGINAL
Parameter t-options
specifies miscellaneous parameters	PARAMETER=
specifies smoothing parameter	SM=
Spline t-options
specifies the degree of the spline	DEGREE=
spaces the knots evenly	EVENLY
specifies the interior knots or break points	KNOTS=
creates n knots	NKNOTS=
Other t-options
renames variables	NAME=
reflects the variable around the mean	REFLECT
specifies transformation standardization	TSTANDARD=

Nonoptimal Transformation t-options

ORIGINAL
ORI: matches the variable's final mean and variance to the mean and variance of the original variable. By default, the mean and variance are based on the transformed values. The ORIGINAL t-option is available for all of the nonoptimal transformations.

Parameter t-options

PARAMETER=number
PAR=number: specifies the transformation parameter. The PARAMETER= t-option is available for the EXP, LOG, POWER, SMOOTH, and SSPLINE transformations. For EXP, the parameter is the value to be exponentiated; for LOG, the parameter is the base value; and for POWER, the parameter is the power. For SMOOTH and SSPLINE, the parameter is the raw smoothing parameter. (You can specify a SAS/GRAPH-style smoothing parameter with the SM= t-option.) The default for the PARAMETER= t-option for the LOG and EXP transformations is e = 2.718 .... The default parameter for SSPLINE is computed from SM=0. For the POWER transformation, you must specify the PARAMETER= t-option; there is no default.
SM=n: specifies a SAS/GRAPH-style smoothing parameter in the range 0 to 100. You can specify the SM= t-option only with the SSPLINE transformation. The smoothness of the function increases as the value of the smoothing parameter increases. By default, SM=0.

Spline t-options

The following t-options are available with the SPLINE and MSPLINE optimal transformations.

DEGREE=n

DEG=n

specifies the degree of the B-spline transformation. The degree must be a nonnegative integer. The defaults are DEGREE=3 for SPLINE variables and DEGREE=2 for MSPLINE variables.

The polynomial degree should be a small integer, usually 0, 1, 2, or 3. Larger values are rarely useful. If you have any doubt as to what degree to specify, use the default.

EVENLY

EVE

is used with the NKNOTS= t-option to space the knots evenly. The differences between adjacent knots are constant. If you specify NKNOTS=k, k knots are created at

minimum + i(( maximum - minimum) / (k + 1))

for i = 1, ... ,k. For example, if you specify

   spline(X / knots=2 evenly)

and the variable X has a minimum of 4 and a maximum of 10, then the two interior knots are 6 and 8. Without the EVENLY t-option, the NKNOTS= t-option places knots at percentiles, so the knots are not evenly spaced.

KNOTS=number-list | n TO m BY p

KNO=number-list | n TO m BY p

specifies the interior knots or break points. By default, there are no knots. The first time you specify a value in the knot list, it indicates a discontinuity in the nth (from DEGREE=n) derivative of the transformation function at the value of the knot. The second mention of a value indicates a discontinuity in the (n-1)th derivative of the transformation function at the value of the knot. Knots can be repeated any number of times for decreasing smoothness at the break points, but the values in the knot list can never decrease.

You cannot use the KNOTS= t-option with the NKNOTS= t-option. You should keep the number of knots small (see the section "Specifying the Number of Knots" in Chapter 65, "The TRANSREG Procedure").

NKNOTS=n

NKN=n

creates n knots, the first at the 100/(n+1) percentile, the second at the 200/(n+1) percentile, and so on. Knots are always placed at data values; there is no interpolation. For example, if NKNOTS=3, knots are placed at the twenty-fifth percentile, the median, and the seventy-fifth percentile. By default, NKNOTS=0. The NKNOTS= t-option must be $\geq 0$ .

You cannot use the NKNOTS= t-option with the KNOTS= t-option. You should keep the number of knots small (see the section "Specifying the Number of Knots" in Chapter 65, "The TRANSREG Procedure").

Other t-options

The following t-options are available for all transformations.

NAME=(variable-list)

NAM=(variable-list)

renames variables as they are used in the TRANSFORM statement. This option allows a variable to be used more than once. For example, if the variable X is a character variable, then the following step stores both the original character variable X and a numeric variable XC that contains category numbers in the output data set.

   proc prinqual data=A n=1 out=B;
      transform linear(Y) opscore(X / name=(XC));
      id X;
   run;

REFLECT

REF

reflects the transformation

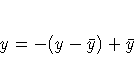
$y = -(y-\bar{y}) + \bar{y}$

after the iterations are completed and before the final standardization and results calculations.

TSTANDARD=CENTER | NOMISS | ORIGINAL | Z

TST=CEN | NOM | ORI | Z

specifies the standardization of the transformed variables in the OUT= data set. By default, TSTANDARD=ORIGINAL. When the TSTANDARD= option is specified in the PROC PRINQUAL statement, it specifies the default standardization for all variables. When you specify TSTANDARD= as a t-option, it overrides the default standardization just for selected variables.

Chapter Contents
Previous
Next
Top