PROC NLMIXED Statement

The NLMIXED Procedure

PROC NLMIXED Statement

PROC NLMIXED options ;

This statement invokes the NLMIXED procedure. A large number of options are available in the PROC NLMIXED statement, and the following table categorizes them according to function.

Table 46.1: PROC NLMIXED statement options

Option	Description
Basic Options
DATA=	input data set
METHOD=	integration method
Displayed Output Specifications
START	gradient at starting values
HESS	Hessian matrix
ITDETAILS	iteration details
CORR	correlation matrix
COV	covariance matrix
ECORR	corr matrix of additional estimates
ECOV	cov matrix of additional estimates
EDER	derivatives of additional estimates
ALPHA=	alpha for confidence limits
DF=	degrees of freedom for p values and confidence limits
Debugging Output
LIST	model program, variables
LISTCODE	compiled model program
LISTDEP	model dependency listing
LISTDER	model derivative
XREF	model cross reference
FLOW	model execution messages
TRACE	detailed model execution messages
Quadrature Options
NOAD	no adaptive centering
NOADSCALE	no adaptive scaling
OUTQ=	output data set
QFAC=	search factor
QMAX=	maximum points
QPOINTS=	number of points
QSCALEFAC=	scale factor
QTOL=	tolerance
Empirical Bayes Options
EBSTEPS=	number of Newton steps
EBSUBSTEPS=	number of substeps
EBSSFRAC=	step-shortening fraction
EBSSTOL=	step-shortening tolerance
EBTOL=	convergence tolerance
EBOPT	comprehensive optimization
EBZSTART	zero starting values
Optimization Specifications
TECHNIQUE=	minimization technique
UPDATE=	update technique
LINESEARCH=	line-search method
LSPRECISION=	line-search precision
HESCAL=	type of Hessian scaling
INHESSIAN=	start for approximated Hessian
RESTART=	iteration number for update restart
OPTCHECK[=]	check optimality in neighborhood
Derivatives Specifications
FD[=]	finite-difference derivatives
FDHESSIAN[=]	finite-difference second derivatives
DIAHES	use only diagonal of Hessian
Constraint Specifications
LCEPSILON=	range for active constraints
LCDEACT=	LM tolerance for deactivating
LCSINGULAR=	tolerance for dependent constraints
Termination Criteria Specifications
MAXFUNC=	maximum number of function calls
MAXITER=	maximum number of iterations
MINITER=	minimum number of iterations
MAXTIME=	upper limit seconds of CPU time
ABSCONV=	absolute function convergence criterion
ABSFCONV=	absolute function convergence criterion
ABSGCONV=	absolute gradient convergence criterion
ABSXCONV=	absolute parameter convergence criterion
FCONV=	relative function convergence criterion
FCONV2=	relative function convergence criterion
GCONV=	relative gradient convergence criterion
XCONV=	relative parameter convergence criterion
FDIGITS=	number accurate digits in objective function
FSIZE=	used in FCONV, GCONV criterion
XSIZE=	used in XCONV criterion
Step Length Specifications
DAMPSTEP[=]	damped steps in line search
MAXSTEP=	maximum trust-region radius
INSTEP=	initial trust-region radius
Singularity Tolerances
SINGCHOL=	tolerance for Cholesky roots
SINGHESS=	tolerance for Hessian
SINGSWEEP=	tolerance for sweep
SINGVAR=	tolerance for variances
Covariance Matrix Tolerances
ASINGULAR=	absolute singularity for inertia
MSINGULAR=	relative M singularity for inertia
VSINGULAR=	relative V singularity for inertia
G4=	threshold for Moore-Penrose inverse
COVSING=	tolerance for singular COV matrix
CFACTOR=	multiplication factor for COV matrix

These options are described in alphabetical order. For a description of the mathematical notation used in the following sections, see the section "Modeling Assumptions and Notation."

ABSCONV=r

ABSTOL=r

specifies an absolute function convergence criterion. For minimization, termination requires $f(\theta^{(k)}) \leq r .$ The default value of r is the negative square root of the largest double precision value, which serves only as a protection against overflows.

ABSFCONV=r[n]

ABSFTOL=r[n]

specifies an absolute function convergence criterion. For all techniques except NMSIMP, termination requires a small change of the function value in successive iterations:

$| f(\theta^{(k-1)}) - f(\theta^{(k)})| \leq r$

The same formula is used for the NMSIMP technique, but $\theta^{(k)}$ is defined as the vertex with the lowest function value, and $\theta^{(k-1)}$ is defined as the vertex with the highest function value in the simplex. The default value is r=0. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process can be terminated.

ABSGCONV=r[n]

ABSGTOL=r[n]

specifies an absolute gradient convergence criterion. Termination requires the maximum absolute gradient element to be small:

$\max_j | g_j(\theta^{(k)})| \leq r$

This criterion is not used by the NMSIMP technique. The default value is r = 1E-5. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process can be terminated.

ABSXCONV=r[n]

ABSXTOL=r[n]

specifies an absolute parameter convergence criterion. For all techniques except NMSIMP, termination requires a small Euclidean distance between successive parameter vectors,

$\parallel \theta^{(k)} - \theta^{(k-1)} \parallel_2 \leq r$

For the NMSIMP technique, termination requires either a small length $\alpha^{(k)}$ of the vertices of a restart simplex,

$\alpha^{(k)} \leq r$

or a small simplex size,

$\delta^{(k)} \leq r$

where the simplex size $\delta^{(k)}$ is defined as the L1 distance from the simplex vertex $\xi^{(k)}$ with the smallest function value to the other n simplex points $\theta_l^{(k)} \neq \xi^{(k)}$ :

$\delta^{(k)} = \sum_{\theta_l \neq y} \parallel \theta_l^{(k)} - \xi^{(k)}\parallel _1$

The default is r = 1E-8 for the NMSIMP technique and r=0 otherwise. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process can terminate.

ALPHA= $\alpha$

specifies the alpha level to be used in computing confidence limits. The default value is 0.05.

ASINGULAR=r

ASING=r

specifies an absolute singularity criterion for the computation of the inertia (number of positive, negative, and zero eigenvalues) of the Hessian and its projected forms. The default value is the square root of the smallest positive double precision value.

CFACTOR=f

specifies a multiplication factor f for the estimated covariance matrix of the parameter estimates.

COV

requests the approximate covariance matrix for the parameter estimates.

CORR

requests the approximate correlation matrix for the parameter estimates.

COVSING=r>0

specifies a nonnegative threshold that determines whether the eigenvalues of a singular Hessian matrix are considered to be zero.

DAMPSTEP[= r]

DS[= r]

specifies that the initial step-size value $\alpha^{(0)}$ for each line search (used by the QUANEW, CONGRA, or NEWRAP technique) cannot be larger than r times the step-size value used in the former iteration. If you specify the DAMPSTEP option without factor r, the default value is r=2. The DAMPSTEP=r option can prevent the line-search algorithm from repeatedly stepping into regions where some objective functions are difficult to compute or where they could lead to floating point overflows during the computation of objective functions and their derivatives. The DAMPSTEP=r option can save time-costly function calls that result in very small step sizes $\alpha$ . For more details on setting the start values of each line search, see the section "Restricting the Step Length," beginning on this page.

DATA=SAS-data-set

specifies the input data set. Observations in this data set are used to compute the log likelihood function that you specify with PROC NLMIXED statements.

NOTE: If you are using a RANDOM statement, the input data set must be clustered according to the SUBJECT= variable. One easy way to accomplish this is to sort your data by the SUBJECT= variable prior to calling PROC NLMIXED. PROC NLMIXED does not sort the input data set for you.

DF=d

specifies the degrees of freedom to be used in computing p values and confidence limits. The default value is the number of subjects minus the number of random effects for random effects models, and the number of observations otherwise.

DIAHES

specifies that only the diagonal of the Hessian is used.

EBOPT

requests that a more comprehensive optimization be carried out if the default empirical Bayes optimization fails to converge.

EBSSFRAC=r>0

specifies the step-shortening fraction to be used while computing empirical Bayes estimates of the random effects. The default value is 0.8.

EBSSTOL= $r \ge 0$

specifies the objective function tolerance for determining the cessation of step-shortening while computing empirical Bayes estimates of the random effects. The default value is r = 1E-8.

EBSTEPS= $n \ge 0$

specifies the maximum number of Newton steps for computing empirical Bayes estimates of random effects. The default value is n=50.

EBSUBSTEPS= $n \ge 0$

specifies the maximum number of step-shortenings for computing empirical Bayes estimates of random effects. The default value is n=20.

EBTOL= $r \ge 0$

specifies the convergence tolerance for empirical Bayes estimation. The default value is $r= \epsilon {\rm E}4$ , where $\epsilon$ is the machine precision. This default value equals approximately 1E-12 on most machines.

EBZSTART

requests that a zero be used as starting values during empirical Bayes estimation. By default, the starting values are set equal to the estimates from the previous iteration (or zero for the first iteration).

ECOV

requests the approximate covariance matrix for all expressions specified in ESTIMATE statements.

ECORR

requests the approximate correlation matrix for all expressions specified in ESTIMATE statements.

EDER

requests the derivatives of all expressions specified in ESTIMATE statements with respect to each of the model parameters.

FCONV=r[n]

FTOL=r[n]

specifies a relative function convergence criterion. For all techniques except NMSIMP, termination requires a small relative change of the function value in successive iterations,

${ | f(\theta^{(k)}) - f(\theta^{(k-1)})| \over \max(| f(\theta^{(k-1)})|,{FSIZE}) } \leq r$

where FSIZE is defined by the FSIZE= option. The same formula is used for the NMSIMP technique, but $\theta^{(k)}$ is defined as the vertex with the lowest function value, and $\theta^{(k-1)}$ is defined as the vertex with the highest function value in the simplex.

The default is r=10^{- FDIGITS} where FDIGITS is the value of the FDIGITS= option. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process can terminate.

FCONV2=r[n]

FTOL2=r[n]

specifies another function convergence criterion. For all techniques except NMSIMP, termination requires a small predicted reduction

$df^{(k)} \approx f(\theta^{(k)}) - f(\theta^{(k)} + s^{(k)})$

of the objective function. The predicted reduction

$df^{(k)} & = & -g^{(k)T} s^{(k)} - {1 \over 2} s^{(k)T} H^{(k)} s^{(k)} \ & = & -{1 \over 2} s^{(k)T} g^{(k)} \ & \leq & r$

is computed by approximating the objective function f by the first two terms of the Taylor series and substituting the Newton step.

s^(k) = - [H^(k)]^-1 g^(k)

For the NMSIMP technique, termination requires a small standard deviation of the function values of the n + 1 simplex vertices $\theta_l^{(k)}$ , l = 0, ... ,n,

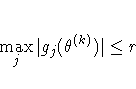
$\sqrt{ {1 \over n+1} \sum_l [ f(\theta_l^{(k)}) - \overline{f}(\theta^{(k)}) ]^2 } \leq r$

where $\overline{f}(\theta^{(k)}) = {1 \over n+1} \sum_l f(\theta_l^{(k)})$ . If there are n_act boundary constraints active at $\theta^{(k)}$ , the mean and standard deviation are computed only for the n + 1 - n_act unconstrained vertices. The default value is r = 1E-6 for the NMSIMP technique and r=0 otherwise. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process can terminate.

FD[= FORWARD | CENTRAL | r]

specifies that all derivatives be computed using finite difference approximations. The following specifications are permitted:

FD

is equivalent to FD=100.

FD=CENTRAL

uses central differences.

FD=FORWARD

uses forward differences.

FD=r

uses central differences for the initial and final evaluations of the gradient, and Hessian. During iteration, start with forward differences and switch to a corresponding central-difference formula during the iteration process when one of the following two criteria is satisfied:

The absolute maximum gradient element is less than or equal to r times the ABSGTOL threshold.
The normalized predicted function reduction (see the GTOL option on this page) is less than or equal to max(1E-6, r * GTOL). The 1E-6 ensures that the switch is done, even if you set the GTOL threshold to zero.

Note that the FD and FDHESSIAN options cannot apply at the same time. The FDHESSIAN option is ignored when only first-order derivatives are used. See the section "Finite Difference Approximations of Derivatives," beginning on this page, for more information.

FDHESSIAN[= FORWARD | CENTRAL]

FDHES[= FORWARD | CENTRAL]

FDH[= FORWARD | CENTRAL]

specifies that second-order derivatives be computed using finite difference approximations based on evaluations of the gradients.

FDHESSIAN=FORWARD: uses forward differences.
FDHESSIAN=CENTRAL: uses central differences.
FDHESSIAN: uses forward differences for the Hessian except for the initial and final output.

Note that the FD and FDHESSIAN options cannot apply at the same time. See the section "Finite Difference Approximations of Derivatives," beginning on this page, for more information.

FDIGITS=r

specifies the number of accurate digits in evaluations of the objective function. Fractional values such as FDIGITS=4.7 are allowed. The default value is $r = - \log_{10} \epsilon$ , where $\epsilon$ is the machine precision. The value of r is used to compute the interval size h for the computation of finite-difference approximations of the derivatives of the objective function and for the default value of the FCONV= option.

FLOW

displays a message for each statement in the model program as it is executed. This debugging option is very rarely needed and produces voluminous output.

FSIZE=r

specifies the FSIZE parameter of the relative function and relative gradient termination criteria. The default value is r=0. For more details, see the FCONV= and GCONV= options.

G4=n>0

specifies a dimension to determine the type of generalized inverse to use when the approximate covariance matrix of the parameter estimates is singular. The default value of n is 60. See the section "Covariance Matrix," beginning on this page, for more information.

GCONV=r[n]

GTOL=r[n]

specifies a relative gradient convergence criterion. For all techniques except CONGRA and NMSIMP, termination requires that the normalized predicted function reduction is small,

${ g(\theta^{(k)})^T [H^{(k)}]^{-1} g(\theta^{(k)}) \over \max(| f(\theta^{(k)})|,{FSIZE}) } \leq r$

where FSIZE is defined by the FSIZE= option. For the CONGRA technique (where a reliable Hessian estimate H is not available), the following criterion is used:

${ \parallel g(\theta^{(k)}) \parallel_2^2 \parallel s(\theta^{(k)}) \parallel_... ...k)}) - g(\theta^{(k-1)}) \parallel_2 \max(| f(\theta^{(k)})|,{FSIZE}) } \leq r$

This criterion is not used by the NMSIMP technique.

The default value is r=1E-8. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process can terminate.

HESCAL=0 | 1 | 2 | 3

HS=0 | 1 | 2 | 3

specifies the scaling version of the Hessian matrix used in NRRIDG, TRUREG, NEWRAP, or DBLDOG optimization. If HS is not equal to 0, the first iteration and each restart iteration sets the diagonal scaling matrix D⁽⁰⁾ = diag(d_i⁽⁰⁾):

$d_i^{(0)} = \sqrt{\max(| H^{(0)}_{i,i}|,\epsilon)}$

where H⁽⁰⁾_i,i are the diagonal elements of the Hessian. In every other iteration, the diagonal scaling matrix D⁽⁰⁾ = diag(d_i⁽⁰⁾) is updated depending on the HS option:

HS=0

specifies that no scaling is done.

HS=1

specifies the Mor $\acute{e}$ (1978) scaling update:

$d_i^{(k+1)} = \max [ d_i^{(k)},\sqrt{\max(| H^{(k)}_{i,i}|, \epsilon)} ]$

HS=2

specifies the Dennis, Gay, & Welsch (1981) scaling update:

$d_i^{(k+1)} = \max [ 0.6 * d_i^{(k)}, \sqrt{\max(| H^{(k)}_{i,i}|,\epsilon)} ]$

HS=3

specifies that d_i is reset in each iteration:

$d_i^{(k+1)} = \sqrt{\max(| H^{(k)}_{i,i}|,\epsilon)}$

In each scaling update, $\epsilon$ is the relative machine precision. The default value is HS=0. Scaling of the Hessian can be time consuming in the case where general linear constraints are active.

HESS

requests the display of the final Hessian matrix after optimization. If you also specify the START option, then the Hessian at the starting values is also printed.

INHESSIAN[= r]

INHESS[= r]

specifies how the initial estimate of the approximate Hessian is defined for the quasi-Newton techniques QUANEW and DBLDOG. There are two alternatives:

If you do not use the r specification, the initial estimate of the approximate Hessian is set to the Hessian at $\theta^{(0)}$ .
If you do use the r specification, the initial estimate of the approximate Hessian is set to the multiple of the identity matrix rI.

By default, if you do not specify the option INHESSIAN=r, the initial estimate of the approximate Hessian is set to the multiple of the identity matrix rI, where the scalar r is computed from the magnitude of the initial gradient.

INSTEP=r

reduces the length of the first trial step during the line search of the first iterations. For highly nonlinear objective functions, such as the EXP function, the default initial radius of the trust-region algorithm TRUREG or DBLDOG or the default step length of the line-search algorithms can result in arithmetic overflows. If this occurs, you should specify decreasing values of 0 < r < 1 such as INSTEP=1E-1, INSTEP=1E-2, INSTEP=1E-4, and so on, until the iteration starts successfully.

For trust-region algorithms (TRUREG, DBLDOG), the INSTEP= option specifies a factor r > 0 for the initial radius $\Delta^{(0)}$ of the trust region. The default initial trust-region radius is the length of the scaled gradient. This step corresponds to the default radius factor of r=1.
For line-search algorithms (NEWRAP, CONGRA, QUANEW), the INSTEP= option specifies an upper bound for the initial step length for the line search during the first five iterations. The default initial step length is r=1.
For the Nelder-Mead simplex algorithm, using TECH=NMSIMP, the INSTEP=r option defines the size of the start simplex.

For more details, see the section "Computational Problems," beginning on this page.

ITDETAILS=

requests a more complete iteration history, including the current values of the parameter estimates, their gradients, and additional optimization statistics. For further details, see the section "Iterations" beginning on this page.

LCDEACT=r

LCD=r

specifies a threshold r for the Lagrange multiplier that determines whether an active inequality constraint remains active or can be deactivated. During minimization, an active inequality constraint can be deactivated only if its Lagrange multiplier is less than the threshold value r < 0. The default value is

r = - min(0.01, max(0.1 * ABSGCONV, 0.001 * gmax^(k)))

where ABSGCONV is the value of the absolute gradient criterion, and gmax^(k) is the maximum absolute element of the (projected) gradient g^(k) or Z^T g^(k). (See the section "Active Set Methods," beginning on this page, for a definition of Z.)

LCEPSILON=r>0

LCEPS=r>0

LCE=r>0

specifies the range for active and violated boundary constraints. The default value is r = 1E-8. During the optimization process, the introduction of rounding errors can force PROC NLMIXED to increase the value of r by a factor of 10,100, .... If this happens, it is indicated by a message displayed in the log.

LCSINGULAR=r>0

LCSING=r>0

LCS=r>0

specifies a criterion r, used in the update of the QR decomposition, that determines whether an active constraint is linearly dependent on a set of other active constraints. The default value is r = 1E-8. The larger r becomes, the more the active constraints are recognized as being linearly dependent. If the value of r is larger than 0.1, it is reset to 0.1.

LINESEARCH=i

LIS=i

specifies the line-search method for the CONGRA, QUANEW, and NEWRAP optimization techniques. Refer to Fletcher (1987) for an introduction to line-search techniques. The value of i can be 1, ... , 8. For CONGRA, QUANEW and NEWRAP, the default value is i = 2.

LIS=1: specifies a line-search method that needs the same number of function and gradient calls for cubic interpolation and cubic extrapolation; this method is similar to one used by the Harwell subroutine library.
LIS=2: specifies a line-search method that needs more function than gradient calls for quadratic and cubic interpolation and cubic extrapolation; this method is implemented as shown in Fletcher (1987) and can be modified to an exact line search by using the LSPRECISION= option.
LIS=3: specifies a line-search method that needs the same number of function and gradient calls for cubic interpolation and cubic extrapolation; this method is implemented as shown in Fletcher (1987) and can be modified to an exact line search by using the LSPRECISION= option.
LIS=4: specifies a line-search method that needs the same number of function and gradient calls for stepwise extrapolation and cubic interpolation.
LIS=5: specifies a line-search method that is a modified version of LIS=4.
LIS=6: specifies golden section line search (Polak 1971), which uses only function values for linear approximation.
LIS=7: specifies bisection line search (Polak 1971), which uses only function values for linear approximation.
LIS=8: specifies the Armijo line-search technique (Polak 1971), which uses only function values for linear approximation.

LIST

displays the model program and variable lists. The LIST option is a debugging feature and is not normally needed.

LISTCODE

displays the derivative tables and the compiled program code. The LISTCODE option is a debugging feature and is not normally needed.

LSPRECISION=r

LSP=r

specifies the degree of accuracy that should be obtained by the line-search algorithms LIS=2 and LIS=3. Usually an imprecise line search is inexpensive and successful. For more difficult optimization problems, a more precise and expensive line search may be necessary (Fletcher 1987). The second line-search method (which is the default for the NEWRAP, QUANEW, and CONGRA techniques) and the third line-search method approach exact line search for small LSPRECISION= values. If you have numerical problems, you should try to decrease the LSPRECISION= value to obtain a more precise line search. The default values are shown in the following table.

TECH=	UPDATE=	LSP default
QUANEW	DBFGS, BFGS	r = 0.4
QUANEW	DDFP, DFP	r = 0.06
CONGRA	all	r = 0.1
NEWRAP	no update	r = 0.9

For more details, refer to Fletcher (1987).

MAXFUNC=i

MAXFU=i

specifies the maximum number i of function calls in the optimization process. The default values are

TRUREG, NRRIDG, NEWRAP: 125
QUANEW, DBLDOG: 500
CONGRA: 1000
NMSIMP: 3000

Note that the optimization can terminate only after completing a full iteration. Therefore, the number of function calls that is actually performed can exceed the number that is specified by the MAXFUNC= option.

MAXITER=i

MAXIT=i

specifies the maximum number i of iterations in the optimization process. The default values are

TRUREG, NRRIDG, NEWRAP: 50
QUANEW, DBLDOG: 200
CONGRA: 400
NMSIMP: 1000

These default values are also valid when i is specified as a missing value.

MAXSTEP=r[n]

specifies an upper bound for the step length of the line-search algorithms during the first n iterations. By default, r is the largest double precision value and n is the largest integer available. Setting this option can improve the speed of convergence for the CONGRA, QUANEW, and NEWRAP techniques.

MAXTIME=r

specifies an upper limit of r seconds of CPU time for the optimization process. The default value is the largest floating point double representation of your computer. Note that the time specified by the MAXTIME= option is checked only once at the end of each iteration. Therefore, the actual running time can be much longer than that specified by the MAXTIME= option. The actual running time includes the rest of the time needed to finish the iteration and the time needed to generate the output of the results.

METHOD=value

specifies the method for approximating the integral of the likelihood over the random effects. Valid values are as follows.

FIRO
specifies the first-order method of Beal and Sheiner (1982).
GAUSS
specifies adaptive Gauss-Hermite quadrature (Pinheiro and Bates 1995). You can prevent the adaptation with the NOAD option or prevent adaptive scaling with the NOADSCALE option. This is the default integration method.
HARDY
specifies Hardy quadrature based on an adaptive trapezoidal rule. This method is available only for one-dimensional integrals; that is, you must specify only one random effect.
ISAMP
specifies adaptive importance sampling (Pinheiro and Bates 1995) . You can prevent the adaptation with the NOAD option or prevent adaptive scaling with the NOADSCALE option. You can use the SEED= option to specify a starting seed for the random number generation used in the importance sampling; otherwise, PROC NLMIXED uses the clock time as a seed.

MINITER=i

MINIT=i

specifies the minimum number of iterations. The default value is 0. If you request more iterations than are actually needed for convergence to a stationary point, the optimization algorithms can behave strangely. For example, the effect of rounding errors can prevent the algorithm from continuing for the required number of iterations.

MSINGULAR=r>0

MSING=r>0

specifies a relative singularity criterion for the computation of the inertia (number of positive, negative, and zero eigenvalues) of the Hessian and its projected forms. The default value is 1E-12 if you do not specify the SINGHESS= option; otherwise, the default value is $\max(10 \epsilon,1{\rm E}-4 * {\rm SINGHESS})$ . See the section "Covariance Matrix," beginning on this page, for more information.

NOAD

requests that the Gaussian quadrature be nonadaptive; that is, the quadrature points are centered at zero for each of the random effects and the current random-effects variance matrix is used as the scale matrix.

NOADSCALE

requests nonadaptive scaling for adaptive Gaussian quadrature; that is, the quadrature points are centered at the empirical Bayes estimates for the the random effects, but the current random-effects variance matrix is used as the scale matrix. By default, the observed Hessian from the current empirical Bayes estimates is used as the scale matrix.

OPTCHECK[= r>0]

computes the function values $f(\theta_l)$ of a grid of points $\theta_l$ in a ball of radius of r about $\theta^*$ .If you specify the OPTCHECK option without factor r, the default value is r=0.1 at the starting point and r=0.01 at the terminating point. If a point $\theta_l^{*}$ is found with a better function value than $f(\theta^{*})$ , then optimization is restarted at $\theta_l^{*}$ .

OUTQ=SAS-data-set

specifies an output data set containing the quadrature points used for numerical integration.

QFAC=r>0

specifies the additive factor used to adaptively search for the number of quadrature points. For METHOD=GAUSS, the search sequence is 1, 3, 5, 7, 9, 11, 11 + r, 11 + 2r, ..., where the default value of r is 10. For METHOD=ISAMP, the search sequence is 10, 10 + r, 10 + 2r, ..., where the default value of r is 50.

QMAX=r>0

specifies the maximum number of quadrature points permitted before the adaptive search is aborted. The default values are 31 for adaptive Gaussian quadrature, 61 for non-adaptive Gaussian quadrature, 160 for adaptive importance sampling, and 310 for non-adaptive importance sampling.

QPOINTS=n>0

specifies the number of quadrature points to be used during evaluation of integrals. For METHOD=GAUSS, n equals the number of points used in each dimension of the random effects, resulting in a total of n^r points, where r is the number of dimensions. For METHOD=ISAMP, n specifies the total number of quadrature points regardless of the dimension of the random effects. By default, the number of quadrature points is selected adaptively, and this option disables the adaptive search.

QSCALEFAC=r>0

specifies a multiplier for the scale matrix used during quadrature calculations. The default value is 1.0.

QTOL=r>0

specifies the tolerance used to adaptively select the number of quadrature points. When the relative difference between two successive likelihood calculations is less than r, then the search terminates and the lesser number of quadrature points is used during the subsequent optimization process. The default value is 1E-4.

RESTART=i>0

REST=i>0

specifies that the QUANEW or CONGRA algorithm is restarted with a steepest descent/ascent search direction after, at most, i iterations. Default values are

CONGRA: UPDATE=PB: restart is performed automatically, i is not used.
CONGRA: UPDATE $\neq$ PB: i = min(10n,80), where n is the number of parameters.
QUANEW: i is the largest integer available.

SEED=i>0

specifies the random number seed for METHOD=ISAMP.

SINGCHOL=r > 0

specifies the singularity criterion r for Cholesky roots of the random-effects variance matrix and scale matrix for adaptive Gaussian quadrature. The default value is 1E4 times the machine epsilon; this product is approximately 1E-12 on most computers.

SINGHESS=r > 0

specifies the singularity criterion r for the inversion of the Hessian matrix. The default value is 1E-8.

See the ASINGULAR, MSINGULAR=, and VSINGULAR= options for more information.

SINGSWEEP=r > 0

specifies the singularity criterion r for inverting the variance matrix in the first-order method and the empirical Bayes Hessian matrix. The default value is 1E4 times the machine epsilon; this product is approximately 1E-12 on most computers.

SINGVAR=r > 0

specifies the singularity criterion r below which statistical variances are considered to equal zero. The default value is 1E4 times the machine epsilon; this product is approximately 1E-12 on most computers.

START

requests that the gradient of the log likelihood at the starting values be displayed. If you also specify the HESS option, then the starting Hessian is displayed as well.

TECHNIQUE=value

TECH=value

specifies the optimization technique. Valid values are

CONGRA
performs a conjugate-gradient optimization, which can be more precisely specified with the UPDATE= option and modified with the LINESEARCH= option. When you specify this option, UPDATE=PB by default.
DBLDOG
performs a version of double dogleg optimization, which can be more precisely specified with the UPDATE= option. When you specify this option, UPDATE=DBFGS by default.
NMSIMP
performs a Nelder-Mead simplex optimization.
NONE
does not perform any optimization. This option can be used
- to perform a grid search without optimization
- to compute estimates and predictions that cannot be obtained efficiently with any of the optimization techniques
NEWRAP
performs a Newton-Raphson optimization combining a line-search algorithm with ridging. The line-search algorithm LIS=2 is the default method.
NRRIDG
performs a Newton-Raphson optimization with ridging.
QUANEW
performs a quasi-Newton optimization, which can be defined more precisely with the UPDATE= option and modified with the LINESEARCH= option. This is the default estimation method.
TRUREG
performs a trust region optimization.

TRACE

displays the result of each operation in each statement in the model program as it is executed. This debugging option is very rarely needed, and it produces voluminous output.

UPDATE=method

UPD=method

specifies the update method for the quasi-Newton, double dogleg, or conjugate-gradient optimization technique. Not every update method can be used with each optimizer. See the section "Optimization Algorithms," beginning on this page, for more information.

Valid methods are

BFGS
performs the original Broyden, Fletcher, Goldfarb, and Shanno (BFGS) update of the inverse Hessian matrix.
DBFGS
performs the dual BFGS update of the Cholesky factor of the Hessian matrix. This is the default update method.
DDFP
performs the dual Davidon, Fletcher, and Powell (DFP) update of the Cholesky factor of the Hessian matrix.
DFP
performs the original DFP update of the inverse Hessian matrix.
PB
performs the automatic restart update method of Powell (1977) and Beale (1972).
FR
performs the Fletcher-Reeves update (Fletcher 1987).
PR
performs the Polak-Ribiere update (Fletcher 1987).
CD
performs a conjugate-descent update of Fletcher (1987).

VSINGULAR=r>0

VSING=r>0

specifies a relative singularity criterion for the computation of the inertia (number of positive, negative, and zero eigenvalues) of the Hessian and its projected forms. The default value is r = 1E-8 if the SINGHESS= option is not specified, and it is the value of SINGHESS= option otherwise. See the section "Covariance Matrix," beginning on this page, for more information.

XCONV=r[n]

XTOL=r[n]

specifies the relative parameter convergence criterion. For all techniques except NMSIMP, termination requires a small relative parameter change in subsequent iterations.

${\max_j |\theta_j^{(k)} - \theta_j^{(k-1)}| \over \max(|\theta_j^{(k)}|,|\theta_j^{(k-1)}|,{XSIZE})} \leq r$

For the NMSIMP technique, the same formula is used, but $\theta_j^{(k)}$ is defined as the vertex with the lowest function value and $\theta_j^{(k-1)}$ is defined as the vertex with the highest function value in the simplex.

The default value is r = 1E-8 for the NMSIMP technique and r=0 otherwise. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process can be terminated.

XSIZE=r>0

specifies the XSIZE parameter of the relative parameter termination criterion. The default value is r=0. For more detail, see the XCONV= option.

Chapter Contents
Previous
Next
Top