Logistic-Normal Model with Binomial Data
This example analyzes the data from Beitler and Landis (1985), which
represent results from a multi-center clinical trial investigating the
effectiveness of two topical cream treatments (active drug, control)
in curing an infection. For each of eight clinics, the number of
trials and favorable cures are recorded for each treatment. The SAS
data set is as follows.
data infection;
input clinic t x n;
datalines;
1 1 11 36
1 0 10 37
2 1 16 20
2 0 22 32
3 1 14 19
3 0 7 19
4 1 2 16
4 0 1 17
5 1 6 17
5 0 0 12
6 1 1 11
6 0 0 10
7 1 1 5
7 0 1 9
8 1 4 6
8 0 6 7
run;
Suppose nij denotes the number of trials for the ith clinic and
the jth treatment (i = 1, ... ,8 j = 0,1), and
xij denotes the corresponding number of favorable cures. Then a
reasonable model for the preceding data is the following logistic
model with random effects:

and
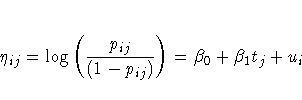
The notation tj indicates the jth treatment, and the ui are
assumed to be iid  .
.The PROC NLMIXED statements to fit this model are as follows:
proc nlmixed data=infection;
parms beta0=-1 beta1=1 s2u=2;
eta = beta0 + beta1*t + u;
expeta = exp(eta);
p = expeta/(1+expeta);
model x ~ binomial(n,p);
random u ~ normal(0,s2u) subject=clinic;
predict eta out=eta;
estimate '1/beta1' 1/beta1;
run;
The PROC NLMIXED statement invokes the procedure, and the PARMS
statement defines the parameters and their starting values. The
next three statements define pij, and the MODEL statement
defines the conditional distribution of xij to be binomial.
The RANDOM statement defines U to be the random effect with subjects
defined by the CLINIC variable.
The PREDICT statement constructs predictions for each observation in
the input data set. For this example, predictions of  and approximate standard errors of prediction are output to a
SAS data set named ETA. These predictions include empirical Bayes
estimates of the random effects ui.
and approximate standard errors of prediction are output to a
SAS data set named ETA. These predictions include empirical Bayes
estimates of the random effects ui.
The ESTIMATE statement requests an estimate of the reciprocal of
 .
.
The output for this model is as follows.
|
| Specifications |
| Data Set |
WORK.INFECTION |
| Dependent Variable |
x |
| Distribution for Dependent Variable |
Binomial |
| Random Effects |
u |
| Distribution for Random Effects |
Normal |
| Subject Variable |
clinic |
| Optimization Technique |
Dual Quasi-Newton |
| Integration Method |
Adaptive Gaussian Quadrature |
|
The "Specifications" table provides basic information about the
nonlinear mixed model.
|
| Dimensions |
| Observations Used |
16 |
| Observations Not Used |
0 |
| Total Observations |
16 |
| Subjects |
8 |
| Max Obs Per Subject |
2 |
| Parameters |
3 |
| Quadrature Points |
5 |
|
The "Dimensions" table provides counts of various variables.
You should check this table to make sure the data set and model have
been entered properly. PROC NLMIXED selects five quadrature points
to achieve the default accuracy in the likelihood calculations.
|
| Parameters |
| beta0 |
beta1 |
s2u |
NegLogLike |
| -1 |
1 |
2 |
37.5945925 |
|
The "Parameters" table lists the starting point of the
optimization.
|
| Iteration History |
| Iter |
|
Calls |
NegLogLike |
Diff |
MaxGrad |
Slope |
| 1 |
|
2 |
37.3622692 |
0.232323 |
2.882077 |
-19.3762 |
| 2 |
|
3 |
37.1460375 |
0.216232 |
0.921926 |
-0.82852 |
| 3 |
|
5 |
37.0300936 |
0.115944 |
0.315897 |
-0.59175 |
| 4 |
|
6 |
37.0223017 |
0.007792 |
0.01906 |
-0.01615 |
| 5 |
|
7 |
37.0222472 |
0.000054 |
0.001743 |
-0.00011 |
| 6 |
|
9 |
37.0222466 |
6.57E-7 |
0.000091 |
-1.28E-6 |
| 7 |
|
11 |
37.0222466 |
5.38E-10 |
2.078E-6 |
-1.1E-9 |
| NOTE: GCONV convergence criterion satisfied. |
|
The "Iterations" table indicates successful convergence in
seven iterations.
|
| Fit Statistics |
| -2 Log Likelihood |
74.0 |
| AIC (smaller is better) |
80.0 |
| BIC (smaller is better) |
80.3 |
| Log Likelihood |
-37.0 |
| AIC (larger is better) |
-40.0 |
| BIC (larger is better) |
-40.1 |
|
The "Fitting Information" table lists some useful statistics
based on the maximized value of the log likelihood.
|
| Parameter Estimates |
| Parameter |
Estimate |
Standard Error |
DF |
t Value |
Pr > |t| |
Alpha |
Lower |
Upper |
Gradient |
| beta0 |
-1.1974 |
0.5561 |
7 |
-2.15 |
0.0683 |
0.05 |
-2.5123 |
0.1175 |
-3.1E-7 |
| beta1 |
0.7385 |
0.3004 |
7 |
2.46 |
0.0436 |
0.05 |
0.02806 |
1.4488 |
-2.08E-6 |
| s2u |
1.9591 |
1.1903 |
7 |
1.65 |
0.1438 |
0.05 |
-0.8554 |
4.7736 |
-2.48E-7 |
|
The "Parameter Estimates" table indicates marginal significance
of the two fixed-effects parameters. The positive value of the
estimate of  indicates that the treatment significantly
increases the chance of a favorable cure.
indicates that the treatment significantly
increases the chance of a favorable cure.
|
| Additional Estimates |
| Label |
Estimate |
Standard Error |
DF |
t Value |
Pr > |t| |
Alpha |
Lower |
Upper |
| 1/beta1 |
1.3542 |
0.5509 |
7 |
2.46 |
0.0436 |
0.05 |
0.05146 |
2.6569 |
|
The "Additional Estimates" table displays results from the
ESTIMATE statement. The estimate of  equals 1/0.7385 =
1.3541 and its standard error equals 0.3004/0.73852 = 0.5509 by
the delta method (Billingsley 1986). Note this particular
approximation produces a t-statistic identical to that for the
estimate of
equals 1/0.7385 =
1.3541 and its standard error equals 0.3004/0.73852 = 0.5509 by
the delta method (Billingsley 1986). Note this particular
approximation produces a t-statistic identical to that for the
estimate of  .
.Not shown is the ETA data set, which contains the original 16
observations and predictions of the  .
.
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.

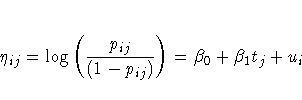
![]() and approximate standard errors of prediction are output to a
SAS data set named ETA. These predictions include empirical Bayes
estimates of the random effects ui.
and approximate standard errors of prediction are output to a
SAS data set named ETA. These predictions include empirical Bayes
estimates of the random effects ui.
![]() .
.![]() .
.