MANOVA Statement

The ANOVA Procedure

MANOVA Statement

MANOVA < test-options >< / detail-options > ;

If the MODEL statement includes more than one dependent variable, you can perform multivariate analysis of variance with the MANOVA statement. The test-options define which effects to test, while the detail-options specify how to execute the tests and what results to display.

When a MANOVA statement appears before the first RUN statement, PROC ANOVA enters a multivariate mode with respect to the handling of missing values; in addition to observations with missing independent variables, observations with any missing dependent variables are excluded from the analysis. If you want to use this mode of handling missing values but do not need any multivariate analyses, specify the MANOVA option in the PROC ANOVA statement.

Test-Options

You can specify the following options in the MANOVA statement as test-options in order to define which multivariate tests to perform.

H=effects | INTERCEPT | _ALL_

specifies effects in the preceding model to use as hypothesis matrices. for multivariate tests For each SSCP matrix H associated with an effect, the H= specification computes an analysis based on the characteristic roots of E^-1H, where E is the matrix associated with the error effect. The characteristic roots and vectors are displayed, along with the Hotelling-Lawley trace, Pillai's trace, Wilks' criterion, and Roy's maximum root criterion with approximate F statistics. Use the keyword INTERCEPT to produce tests for the intercept. To produce tests for all effects listed in the MODEL statement, use the keyword _ALL_ in place of a list of effects. For background and further details, see the "Multivariate Analysis of Variance" section in Chapter 30, "The GLM Procedure."

E=effect

specifies the error effect. If you omit the E= specification, the ANOVA procedure uses the error SSCP (residual) matrix from the analysis.

M=equation,...,equation | (row-of-matrix,...,row-of-matrix)

specifies a transformation matrix for the dependent variables listed in the MODEL statement. The equations in the M= specification are of the form

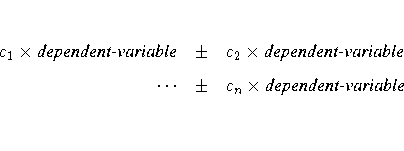
$c_1 x {{dependent-variable}} & +- & c_2 x {{dependent-variable}} \ ... & +- & c_n x {{dependent-variable}} \$

where the c_i values are coefficients for the various dependent-variables. If the value of a given c_i is 1, it may be omitted; in other words 1 ×Y is the same as Y. Equations should involve two or more dependent variables. For sample syntax, see the "Examples" section.

Alternatively, you can input the transformation matrix directly by entering the elements of the matrix with commas separating the rows, and parentheses surrounding the matrix. When this alternate form of input is used, the number of elements in each row must equal the number of dependent variables. Although these combinations actually represent the columns of the M matrix, they are displayed by rows.

When you include an M= specification, the analysis requested in the MANOVA statement is carried out for the variables defined by the equations in the specification, not the original dependent variables. If you omit the M= option, the analysis is performed for the original dependent variables in the MODEL statement.

If an M= specification is included without either the MNAMES= or the PREFIX= option, the variables are labeled MVAR1, MVAR2, and so forth by default. For further information, see the section "Multivariate Analysis of Variance" in Chapter 30, "The GLM Procedure."

MNAMES=names

provides names for the variables defined by the equations in the M= specification. Names in the list correspond to the M= equations or the rows of the M matrix (as it is entered).

PREFIX=name

is an alternative means of identifying the transformed variables defined by the M= specification. For example, if you specify PREFIX=DIFF, the transformed variables are labeled DIFF1, DIFF2, and so forth.

Detail-Options

You can specify the following options in the MANOVA statement after a slash as detail-options:

CANONICAL

produces a canonical analysis of the H and E matrices (transformed by the M matrix, if specified) instead of the default display of characteristic roots and vectors.

ORTH

requests that the transformation matrix in the M= specification of the MANOVA statement be orthonormalized by rows before the analysis.

PRINTE

displays the error SSCP matrix E. If the E matrix is the error SSCP (residual) matrix from the analysis, the partial correlations of the dependent variables given the independent variables are also produced.

For example, the statement

   manova / printe;

displays the error SSCP matrix and the partial correlation matrix computed from the error SSCP matrix.

PRINTH

displays the hypothesis SSCP matrix H associated with each effect specified by the H= specification.

SUMMARY

produces analysis-of-variance tables for each dependent variable. When no M matrix is specified, a table is produced for each original dependent variable from the MODEL statement; with an M matrix other than the identity, a table is produced for each transformed variable defined by the M matrix.

Examples

The following statements give several examples of using a MANOVA statement.

   proc anova;
      class A B;
      model Y1-Y5=A B(A);
      manova h=A e=B(A) / printh printe;
      manova h=B(A) / printe;
      manova h=A e=B(A) m=Y1-Y2,Y2-Y3,Y3-Y4,Y4-Y5
             prefix=diff;



      manova h=A e=B(A) m=(1 -1  0  0  0,
                           0  1 -1  0  0,
                           0  0  1 -1  0,
                           0  0  0  1 -1) prefix=diff;
   run;

The first MANOVA statement specifies A as the hypothesis effect and B(A) as the error effect. As a result of the PRINTH option, the procedure displays the hypothesis SSCP matrix associated with the A effect; and, as a result of the PRINTE option, the procedure displays the error SSCP matrix associated with the B(A) effect.

The second MANOVA statement specifies B(A) as the hypothesis effect. Since no error effect is specified, PROC ANOVA uses the error SSCP matrix from the analysis as the E matrix. The PRINTE option displays this E matrix. Since the E matrix is the error SSCP matrix from the analysis, the partial correlation matrix computed from this matrix is also produced.

The third MANOVA statement requests the same analysis as the first MANOVA statement, but the analysis is carried out for variables transformed to be successive differences between the original dependent variables. The PREFIX=DIFF specification labels the transformed variables as DIFF1, DIFF2, DIFF3, and DIFF4.

Finally, the fourth MANOVA statement has the identical effect as the third, but it uses an alternative form of the M= specification. Instead of specifying a set of equations, the fourth MANOVA statement specifies rows of a matrix of coefficients for the five dependent variables.

As a second example of the use of the M= specification, consider the following:

   proc anova;
      class group;
      model dose1-dose4=group / nouni;
      manova h = group
             m = -3*dose1 -   dose2 +   dose3 + 3*dose4,
                    dose1 -   dose2 -   dose3 +   dose4,
                   -dose1 + 3*dose2 - 3*dose3 +   dose4
             mnames = Linear Quadratic Cubic
             / printe;
   run;

The M= specification gives a transformation of the dependent variables dose1 through dose4 into orthogonal polynomial components, and the MNAMES= option labels the transformed variables as LINEAR, QUADRATIC, and CUBIC, respectively. Since the PRINTE option is specified and the default residual matrix is used as an error term, the partial correlation matrix of the orthogonal polynomial components is also produced.

For further information, see the "Multivariate Analysis of Variance" section in Chapter 30, "The GLM Procedure."

Chapter Contents
Previous
Next
Top