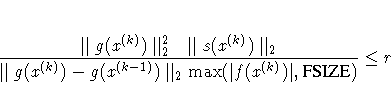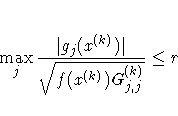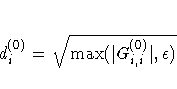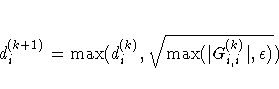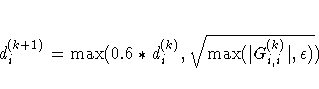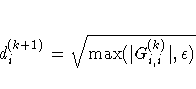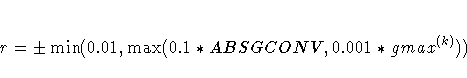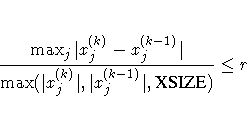PROC NLP Statement
This statement invokes the NLP procedure.
- PROC NLP options ;
The following options are used with the PROC NLP statement.
-
ABSCONV=r
- ABSTOL=r
-
specifies an absolute function convergence criterion.
For minimization (maximization), termination requires
 The default value of ABSTOL is
the negative (positive) square root
of the largest double precision value.
The default value of ABSTOL is
the negative (positive) square root
of the largest double precision value.
-
ABSFCONV =r[n]
- ABSFTOL=r[n]
-
specifies an absolute function convergence criterion. For all techniques
except NMSIMP, termination requires a small change of the
function value in successive iterations:
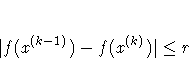
For the NMSIMP technique the same formula is used, but
x(k) is defined as the vertex with the lowest function
value, and x(k-1) is defined as the vertex with the highest
function value in the simplex. The default value is r=0.
The optional integer value n specifies the number of successive
iterations for which the criterion must be satisfied before the
process can be terminated.
-
ABSGCONV=r[n]
- ABSGTOL=r[n]
-
specifies the absolute
gradient convergence criterion. Termination requires the maximum
absolute gradient element to be small:
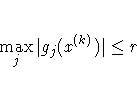
This criterion is not used by the NMSIMP technique. The default
value is r=1e-5.
The optional integer value n specifies the number of successive
iterations for which the criterion must be satisfied before the
process can be terminated.
-
ABSXCONV=r[n]
- ABSXTOL=r[n]
-
specifies the
absolute parameter convergence criterion. For all techniques
except NMSIMP, termination requires a small Euclidean distance
between successive parameter vectors,
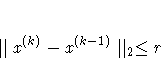
For the NMSIMP technique, termination requires either a small
length  of the vertices of a restart simplex
of the vertices of a restart simplex
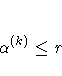
or a small simplex size
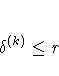
where the simplex size  is defined as the L1 distance
of the simplex vertex y(k) with the smallest function value
to the other n simplex points
is defined as the L1 distance
of the simplex vertex y(k) with the smallest function value
to the other n simplex points  :
:
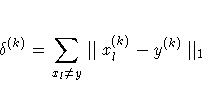
The default value is r=1e-4 for the COBYLA NMSIMP technique,
r=1e-8 for the standard NMSIMP technique, and r=0 otherwise.
The optional integer value n specifies the number of successive
iterations for which the criterion must be satisfied before the
process can be terminated.
-
ASINGULAR=r
- ASING=r
-
specifies an absolute singularity
criterion for measuring singularity
of Hessian and crossproduct Jacobian and their projected
forms, which may have to be converted to compute the
covariance matrix. The default is the square
root of the smallest positive double precision value.
For more information, see the section "Covariance Matrix".
-
BEST=i
-
produces the i best grid points only.
This option not only restricts the output, it also can
significantly reduce the computation time needed for sorting
the grid point information.
-
CDIGITS=r
-
specifies the number of accurate digits
in nonlinear constraint evaluations. Fractional values such as
CDIGITS=4.7 are allowed. The default value is r=-log10(
 ),
where
),
where  is the machine precision. The value of r is
used to compute the interval size h for the computation of
finite-difference approximations of the Jacobian matrix
of nonlinear constraints.
is the machine precision. The value of r is
used to compute the interval size h for the computation of
finite-difference approximations of the Jacobian matrix
of nonlinear constraints.
-
CLPARM= PL | WALD | BOTH
-
The CLPARM = option is similar to but
not the same as that used by other SAS procedures.
Using CLPARM=BOTH is equivalent to specifying
PROFILE / ALPHA=0.5 0.1 0.05 0.01 OUTTABLE;
and specifies that PL CLs for all parameters and for
 are computed and displayed or written
to the OUTEST= data set. Computing the profile confidence
limits for all parameters
can be very expensive and should be avoided when a difficult
optimization problem or one with many parameters is solved.
The OUTTABLE option is valid only when an OUTEST= data set is
specified in the PROC NLP statement.
For CLPARM=BOTH, the table of displayed output contains
the Wald confidence limits computed from the standard errors as
well as the PL CLs. The Wald confidence limits are not computed
(displayed or written to the OUTEST= data set) unless the
approximate covariance matrix of parameters is computed.
are computed and displayed or written
to the OUTEST= data set. Computing the profile confidence
limits for all parameters
can be very expensive and should be avoided when a difficult
optimization problem or one with many parameters is solved.
The OUTTABLE option is valid only when an OUTEST= data set is
specified in the PROC NLP statement.
For CLPARM=BOTH, the table of displayed output contains
the Wald confidence limits computed from the standard errors as
well as the PL CLs. The Wald confidence limits are not computed
(displayed or written to the OUTEST= data set) unless the
approximate covariance matrix of parameters is computed.
-
COVARIANCE=1 | 2 | 3 | 4 | 5 | 6 | M | H | J | B | E | U
- COV=1 | 2 | 3 | 4 | 5 | 6 | M | H | J | B | E | U
-
specifies one of
six formulas for computing the covariance matrix.
For more information, see the section "Covariance Matrix".
-
COVSING=r>0
-
specifies a threshold that
determines whether the eigenvalues of a singular Hessian matrix
or crossproduct Jacobian matrix are considered to be zero.
For more information, see the section "Covariance Matrix".
-
DAMPSTEP[=r]
- DS[=r]
-
specifies that the
initial step size value
 for each line-search
(used by the QUANEW, HYQUAN, CONGRA, or NEWRAP technique) cannot be larger
than r times the step size value used in the former
iteration. If the DAMPSTEP option is specified but not factor r,
the default is r=2. The DAMPSTEP=r option can prevent the
line-search algorithm from repeatedly stepping into
regions where some objective functions are difficult to compute
or where they could lead to floating point overflows during the
computation of objective functions and their derivatives.
The DAMPSTEP=r option can save time-costly function calls
during the line-searches of objective functions that result
in very small step. For more information, see the section "Restricting the Step Length".
for each line-search
(used by the QUANEW, HYQUAN, CONGRA, or NEWRAP technique) cannot be larger
than r times the step size value used in the former
iteration. If the DAMPSTEP option is specified but not factor r,
the default is r=2. The DAMPSTEP=r option can prevent the
line-search algorithm from repeatedly stepping into
regions where some objective functions are difficult to compute
or where they could lead to floating point overflows during the
computation of objective functions and their derivatives.
The DAMPSTEP=r option can save time-costly function calls
during the line-searches of objective functions that result
in very small step. For more information, see the section "Restricting the Step Length".
-
DATA=SAS-data-set
-
allows variables from the specified data set
to be used in the specification of the objective function f.
For more information, see the section "DATA= Input Data Set".
-
DIAHES
-
specifies that only the diagonal of the
Hessian or crossproduct Jacobian is used.
This saves function evaluations but may considerably
slow the convergence process. Note that the
DIAHES option refers to both the Hessian and the crossproduct
Jacobian when using the LSQ statement. When derivatives are
specified using the HESSIAN or CRPJAC statement, these
statements must refer only to the n diagonal derivative
elements (otherwise, the n(n+12)/2 derivatives of the lower
triangle must be specified). The DIAHES option is ignored if a
quadratic programming with a constant Hessian is specified by
TECH=QUADAS or TECH=LICOMP.
-
FCONV =r[n]
- FTOL=r[n]
-
specifies the relative
function convergence criterion. For all techniques except NMSIMP,
termination requires a small relative change of the function
value in successive iterations,
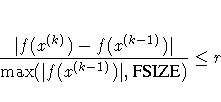
where FSIZE is defined by the FSIZE= option.
For the NMSIMP technique, the same formula is used, but
x(k) is defined as the vertex with the lowest function
value, and x(k-1) is defined as the vertex with the highest
function value in the simplex.
The default value is r=10- FDIGITS
where FDIGITS is the value of the FDIGITS= option.
The optional integer value n specifies the number of successive
iterations for which the criterion must be satisfied before the
process can be terminated.
-
FCONV 2=r[n]
- FTOL2=r[n]
-
specifies another
function convergence criterion.
For least-squares problems and all techniques except NMSIMP,
termination requires a small predicted reduction
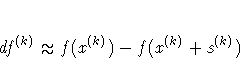
of the objective function. The predicted reduction
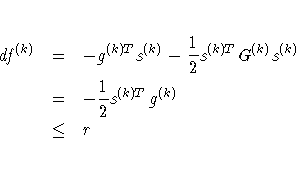
is based on approximating the objective function f
by the first two terms of the Taylor series and substituting
the Newton step
-
s(k) = - G(k)-1 g(k)
For the NMSIMP technique, termination requires a small standard
deviation of the function values of the n + 1 simplex vertices
xl(k), l = 0, ... ,n,
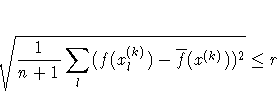
where  .If there are nact boundary constraints active at x(k),
the mean and standard deviation are computed only for the
n + 1 - nact unconstrained vertices.
The default value is r=1e-6 for the NMSIMP technique and the
QUANEW technique with nonlinear constraints and r=0 otherwise.
The optional integer value n specifies the number of successive
iterations for which the criterion must be satisfied before the
process can be terminated.
.If there are nact boundary constraints active at x(k),
the mean and standard deviation are computed only for the
n + 1 - nact unconstrained vertices.
The default value is r=1e-6 for the NMSIMP technique and the
QUANEW technique with nonlinear constraints and r=0 otherwise.
The optional integer value n specifies the number of successive
iterations for which the criterion must be satisfied before the
process can be terminated.
-
FD[=FORWARD | CENTRAL | number]
-
specifies that all derivatives
be computed using finite difference
approximations.
The following specifications are permitted:
- FD=FORWARD
- uses forward differences.
- FD=CENTRAL
- uses central differences.
- FD=number
- uses central differences for the initial
and final evaluations of the gradient, Jacobian, and
Hessian. During iteration, start with forward differences
and switch to a corresponding central-difference formula
during the iteration process when one of the following
two criteria is satisfied:
- The absolute maximum gradient element is less than
or equal to number times the ABSGTOL threshold.
- The term left of the GTOL criterion is less than or
equal to max(1.0E-6,number*GTOL threshold). The
1.0E-6 ensures that the switch is done, even if you
set the GTOL threshold to zero.
- FD
- is equivalent to FD=100.
Note that the FD and FDHESSIAN options cannot apply at the same time.
The FDHESSIAN option is ignored when only first-order
derivatives are used, for example, when the LSQ statement
is used and the HESSIAN is not explicitly needed (displayed
or written to a data set).
For more information, see the section "Finite-Difference Approximations of Derivatives".
-
FDHESSIAN[=FORWARD | CENTRAL]
- FDHES[=FORWARD | CENTRAL]
- FDH[=FORWARD | CENTRAL]
-
specifies that second-order derivatives
be computed using finite difference approximations based on evaluations
of the gradients.
- FDHESSIAN=FORWARD
- uses forward differences.
- FDHESSIAN=CENTRAL
- uses central differences.
- FDHESSIAN
- uses forward differences
for the Hessian except for the initial and final
output.
Note that the FD and FDHESSIAN options cannot apply at the same time.
For more information, see the section "Finite-Difference Approximations of Derivatives"
-
FDIGITS=r
-
specifies the number of accurate digits
in evaluations of the objective function. Fractional values
such as FDIGITS=4.7 are allowed. The default value is r=-log10(
 ),
where
),
where  is the machine precision. The value of r is
used to compute the interval size h for the computation of
finite-difference approximations of the derivatives of the
objective function and for the default value of the FCONV =
option.
is the machine precision. The value of r is
used to compute the interval size h for the computation of
finite-difference approximations of the derivatives of the
objective function and for the default value of the FCONV =
option.
-
FDINT= OBJ | CON | ALL
-
specifies how the finite difference
intervals h should be computed.
For FDINT=OBJ, the interval h is based on the behavior of
the objective function; for FDINT=CON, the interval h
is based on the behavior of the nonlinear constraints
functions; and for FDINT=ALL, the interval h is based
on the behavior of the objective function and the
nonlinear constraints functions.
For more information, see the section "Finite-Difference Approximations of Derivatives".
-
FSIZE=r
-
specifies the FSIZE parameter of the relative
function and relative gradient termination criteria. The default
value is r=0. For more details, see the FCONV = and GCONV= options
in the the section "PROC NLP Statement".
-
G4=n>0
-
The G4= option is used when the covariance matrix is singular.
The value n determines which generalized inverse is computed.
The default value of n is 60.
For more information, see the section "Covariance Matrix".
-
GCONV=r[n]
- GTOL=r[n]
-
specifies the relative
gradient convergence criterion. For all techniques except the
CONGRA and NMSIMP techniques, termination requires that the
normalized predicted function reduction is small,
![{ g(x^{(k)})^T [G^{(k)}]^{-1} g(x^{(k)}) \over
\max(| f(x^{(k)})|,{FSIZE}) } \leq r](images/nlpeq32.gif)
where FSIZE is defined by the FSIZE= option.
For the CONGRA technique (where a reliable Hessian estimate G
is not available)
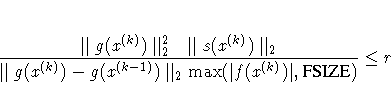
is used. This criterion is not used by the NMSIMP technique.
The default value is r=1e-8.
The optional integer value n speicfies the number of successive
iterations for which the criterion must be satisfied before the
process can be terminated.
-
GCONV2=r[n]
- GTOL2=r[n]
-
specifies another relative gradient convergence criterion.
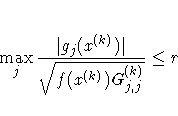
This option is valid only when using the
TRUREG, LEVMAR, NRRIDG, and NEWRAP techniques on least-squares problems.
The default value is r=0.
The optional integer value n specifies the number of successive
iterations for which the criterion must be satisfied before the
process can be terminated.
-
GRADCHECK[= NONE | FAST | DETAIL]
- GC[= NONE | FAST | DETAIL]
-
Specifying
GRADCHECK= DETAIL computes a test vector and test matrix
to check whether the gradient g specified by a
GRADIENT (or indirectly by a JACOBIAN) statement is appropriate
for the function f computed by the program statements.
If the specification of the first derivatives is correct, the
elements of the test vector and test matrix should be relatively
small. For very large optimization problems, the algorithm can be
too expensive in terms of computer time and memory. If the GRADCHECK
option is not specified, a fast derivative test identical
to the GRADCHECK= FAST specification is performed by default.
It is possible to
suppress the default derivative test by specifying GRADCH=NONE.
For more information, see the section "Testing the Gradient Specification".
-
HESCA=0 | 1 | 2 | 3
- HS=0 | 1 | 2 | 3
-
specifies the scaling
version of the Hessian or crossproduct Jacobian matrix used in
NRRIDG, TRUREG, LEVMAR, NEWRAP, or DBLDOG optimization.
If the value of the HS=option is not equal to zero, the first iteration and each restart
iteration sets the diagonal scaling matrix D(0)=diag(di(0)):
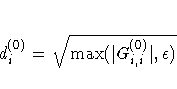
where G(0)i,i are the diagonal elements of the
Hessian or crossproduct Jacobian matrix.
In every other iteration, the diagonal scaling matrix
D(0)=diag(di(0)) is updated depending on the HS=option:
- HS=0
- specifies that no scaling is done.
- HS=1
- specifies the Mor
 (1978) scaling update:
(1978) scaling update:
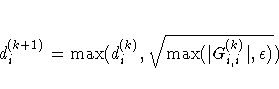
- HS=2
- specifies the Dennis, Gay, & Welsch (1981) scaling update:
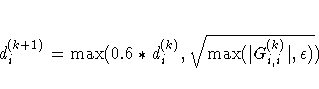
- HS=3
- specifies that di is reset in each iteration:
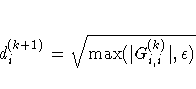
where  is the relative machine precision.
The default value is HS=1 for LEVMAR minimization and HS=0 otherwise.
Scaling of the Hessian or crossproduct Jacobian matrix can be
time-consuming in the case where general linear constraints
are active.
is the relative machine precision.
The default value is HS=1 for LEVMAR minimization and HS=0 otherwise.
Scaling of the Hessian or crossproduct Jacobian matrix can be
time-consuming in the case where general linear constraints
are active.
-
INEST=SAS-data-set
- INVAR=SAS-data-set
- ESTDATA=SAS-data-set
-
can be used to specify the initial values of the parameters
defined in a PARMS or VAR statement as well as simple boundary
constraints and general linear constraints. The INEST= data set
can contain additional variables with names corresponding to
constants used in the program statements. At the beginning of each
run of PROC NLP, the values of the constants are read from the
PARMS observation, initializing the constants in the program
statements. For more information, see the section "INEST= Input Data Set".
-
INFEASIBLE
- IFP
-
specifies that the
function values of both feasible and infeasible grid points are
to be computed, displayed, and written to the OUTEST= or OUTVAR=
data set, although only the feasible grid points are candidates
for the starting point x(0). This option enables you to explore
the shape of the objective function of points surrounding the
feasible region. For the output, the grid points are
sorted first with decreasing values of the maximum constraint
violation. Points with the same value of the maximum constraint
violation are then sorted with increasing (minimization) or
decreasing (maximization) value of the objective function.
Using the BEST= option restricts only the number of best grid
points in the displayed output, not those in the data set. The
INFEASIBLE option affects both the displayed output and the
output saved to the OUTEST= data set. The OUTGRID option can be used
to write the grid points and their function values to an OUTEST= or
OUTVAR= data set. After small modifications (deleting unneeded
information), this data set can be used with the G3D procedure of the
SAS/GRAPHproduct to generate a three-dimensional surface plot
of the objective function depending on two selected parameters.
For more information on grids, see the section "DECVAR Statement".
-
INHESSIAN[=r]
- INHESS[=r]
-
specifies how the initial
estimate of the approximate Hessian is defined for the quasi-Newton
techniques QUANEW, DBLDOG, and HYQUAN. There are two alternatives:
- The =r specification is not used: the initial estimate of the
approximate Hessian is set to the true Hessian or crossproduct
Jacobian at x(0).
- The =r specification is used: the initial estimate of the
approximate Hessian is set to the multiple of the identity
matrix rI.
By default, if INHESSIAN=r is not specified, the initial estimate
of the approximate Hessian is set to the multiple of the identity
matrix rI, where the scalar r is computed from the magnitude
of the initial gradient.
For most applications, this is a sufficiently good
first approximation.
-
INITIAL=r
-
specifies a value r as the common
initial value for all parameters for which no other initial
value assignments by the PARMS or VAR statement or an INEST=
(or INVAR= or ESTDATA=) data set are made.
For more information, see the description of the INITIAL
option in the section "PROC NLP Statement".
-
INQUAD=SAS-data-set
-
can be used to specify (the nonzero
elements of) the matrix H, vector g, and scalar c of
a quadratic programming problem,
 .This option cannot be used together with the NLINCON statement.
Two forms (dense and sparse) of the INQUAD= data
set can be used. For more information,see the section "INQUAD= Input Data Set".
.This option cannot be used together with the NLINCON statement.
Two forms (dense and sparse) of the INQUAD= data
set can be used. For more information,see the section "INQUAD= Input Data Set".
-
INSTEP=r
-
For highly nonlinear objective functions, such as the EXP function,
the default initial radius of the trust-region algorithm TRUREG,
DBLDOG, or LEVMAR or the default step length of the line-search
algorithms can result in arithmetic overflows. If this occurs,
decreasing values of 0 < r < 1 should be specified, such as INSTEP=1e-1,
INSTEP=1e-2, INSTEP=1e-4, and so on, until the iteration starts
successfully.
- For trust-region algorithms (TRUREG, DBLDOG, LEVMAR)
the INSTE=P option specifies a factor r > 0 for the initial radius
 of the trust region. The default initial trust-region radius is
the length of the scaled gradient. This step corresponds to the
default radius factor of r=1.
of the trust region. The default initial trust-region radius is
the length of the scaled gradient. This step corresponds to the
default radius factor of r=1.
- For line-search algorithms (NEWRAP, CONGRA, QUANEW, HYQUAN)
the INSTEP= option specifies an upper bound for the initial step length for
the line-search during the first five iterations. The default
initial step length is r=1.
- For the Nelder-Mead simplex algorithm,
using TECH= NMSIMP, the INSTEP=r option defines the size of
the initial simplex.
For more details, see the section "Computational Problems".
-
LCDEACT=r
- LCD=r
-
specifies a threshold r for the Lagrange multiplier that decides
whether an active inequality constraint remains active or can
be deactivated. For a maximization (minimization), an active
inequality constraint can be deactivated only if its Lagrange
multiplier is greater (less) than the threshold value r.
For maximization, r must be greater than zero;
for minimization, r must be smaller than zero. The default value is
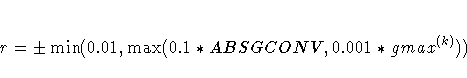
where the + stands for maximization, the - for minimization,
ABSGCONV is the value of the absolute gradient criterion, and
gmax(k) is the maximum absolute element of the (projected)
gradient g(k) or ZT g(k).
-
LCEPSILON=r>0
- LCEPS=r>0
- LCE=r>0
-
specifies the range
for active and violated boundary and linear
constraints.
During the optimization process, the
introduction of rounding errors can force PROC NLP to
increase the value of r by a factor of 10, 100,... If
this happens it is indicated by a message written to the log.
For more information, see the section "Linear Complementarity (LICOMP)".
-
LCSINGULAR=r>0
- LCSING=r>0
- LCS=r>0
-
specifies a criterion r used in the update of
the QR decomposition that decides whether an active
constraint is linearly dependent on a set of other active
constraints. The default value is r=1e-8. The larger r becomes,
the more the active constraints are recognized as being
linearly dependent. If the value of r is larger than
0.1, it is reset to 0.1.
-
LINESEARCH=i
- LIS=i
-
specifies the
line-search method for the CONGRA, QUANEW, HYQUAN, and NEWRAP
optimization techniques.
Refer to Fletcher (1987)
for an introduction to
line-search techniques. The value of i can be 1, ... , 8.
For CONGRA, QUANEW, and NEWRAP, the default value is i = 2. A special
line-search method is the default for the least-squares technique
HYQUAN that is based on an algorithm developed by Lindstr
 m
& Wedin (1984). Although it needs more memory, this default
line-search method sometimes works better with large
least-squares problems. However, by specifying LIS=i,
i = 1, ... , 8, it is possible to use one of the standard
techniques with HYQUAN.
m
& Wedin (1984). Although it needs more memory, this default
line-search method sometimes works better with large
least-squares problems. However, by specifying LIS=i,
i = 1, ... , 8, it is possible to use one of the standard
techniques with HYQUAN.
- LIS=1
- specifies a line-search method that needs the
same number of function and gradient calls for
cubic interpolation and cubic extrapolation.
- LIS=2
- specifies a line-search method that needs more
function than gradient calls for quadratic and
cubic interpolation and cubic extrapolation;
this method is implemented as shown in
Fletcher (1987) and can be modified to an exact
line-search by using the LSPRECISION= option.
- LIS=3
- specifies a line-search method that needs the
same number of function and gradient calls for
cubic interpolation and cubic extrapolation;
this method is implemented as shown in
Fletcher (1987) and can be modified to an exact
line-search by using the LSPRECISION= option.
- LIS=4
- specifies a line-search method that needs the
same number of function and gradient calls for
stepwise extrapolation and cubic interpolation.
- LIS=5
- specifies a line-search method that is a modified
version of LIS=4.
- LIS=6
- specifies golden section line-search (Polak 1971), which
uses only function values for linear approximation.
- LIS=7
- specifies bisection line-search (Polak 1971), which
uses only function values for linear approximation.
- LIS=8
- specifies the Armijo line-search technique, (Polak 1971)
which uses only function values for linear approximation.
-
LIST
-
displays the model program and variable lists.
The LIST option is a debugging feature and is not normally needed. This
output is not included in either the default output or
the output specified by the PALL option.
-
LISTCODE
-
diplays the derivative tables and the compiled
program code. The LISTCODE option is a debugging feature and is not normally
needed. This output is not included in either the default
output or the output specified by the PALL option. The option is
similar to that used in MODEL procedure in SAS/ETS software.
-
LSPRECISION=r
- LSP=r
-
specifies the
degree of accuracy that should be obtained by the line-search
algorithms LIS=2 and LIS=3. Usually an imprecise line-search
is inexpensive and sufficient for convergence to the optimum.
For difficult optimization
problems, a more precise and expensive line-search may be
necessary (Fletcher
1987). The second (default
for NEWRAP, QUANEW, and CONGRA) and third line-search methods
approach exact line-search for small LSPRECISION= values.
In the presence of numerical problems, it is advised to decrease
the LSPRECISION= value to obtain a more precise line-search.
The default values are as follows.
|
TECH=
|
UPDATE=
|
LSP default
|
| QUANEW | DBFGS, BFGS | r = 0.4 |
| QUANEW | DDFP, DFP | r = 0.06 |
| HYQUAN | DBFGS | r = 0.1 |
| HYQUAN | DDFP | r = 0.06 |
| CONGRA | all | r = 0.1 |
| NEWRAP | no update | r = 0.9 |
For more details, refer to Fletcher
(1987).
-
MAXFUNC=i
- MAXFU=i
-
specifies the
maximum number i of function calls in the optimization
process. The default values are
- TRUREG, LEVMAR, NRRIDG, NEWRAP: 125
- QUANEW, HYQUAN, DBLDOG: 500
- CONGRA, QUADAS: 1000
- NMSIMP: 3000
Note that the optimization can be terminated only after
completing a full iteration. Therefore, the number of function
calls that are actually performed can exceed the number that
is specified by the MAXFUNC= option.
-
MAXITER=i[n]
- MAXIT=i[n]
-
specifies the
maximum number i of iterations in the optimization process.
The default values are:
- TRUREG, LEVMAR, NRRIDG, NEWRAP: 50
- QUANEW, HYQUAN, DBLDOG: 200
- CONGRA, QUADAS: 400
- NMSIMP: 1000
This default value is valid also when i is specified as
a missing value. The optional second value n is valid only
for TECH= QUANEW with nonlinear constraints. It specifies an
upper bound n for the number of iterations of an algorithm
used to reduce the violation of nonlinear constraints at a
starting point. The default value is n=20.
-
MAXSTEP=r[n]
-
specifies an upper bound for the
step length of the line-search algorithms during the
first n iterations. By default, r is the largest
double precision value and n is the largest integer
available. Setting this option can reduce the speed of
convergence for TECH=CONGRA, TECH=QUANEW, TECH=HYQUAN, and TECH=NEWRAP.
-
MAXTIME=r
-
specifies an upper limit of r seconds of
CPU time for the optimization process. The default value is the largest
floating point double representation of the computer. Note that
the time specified by the MAXTIME= option is checked only once at
the end of each iteration. Therefore, the actual running time of
the PROC NLP job may be longer than that specified by the
MAXTIME= option. The actual running time includes the rest of the
time needed to finish the iteration, time for the output
of the (temporary) results, and (if required) the time for saving
the results in an OUTEST= or OUTVAR= data set. Using the MAXTIME=
option with a permanent OUTEST= data set enables you to separate
large optimization problems into a series of smaller problems
that need smaller amounts of CPU time.
-
MINITER=i
- MINIT=i
-
specifies the
minimum number of iterations. The default value is zero.
If more iterations than are actually needed are requested for
convergence to a stationary point, the optimization
algorithms can behave strangely.
For example,the effect of
rounding errors can prevent the algorithm from continuing
for the required number of iterations.
-
MODEL=model-name, model-list
- MOD=model-name, model-list
- MODFILE=model-name, model-list
-
reads the program statements from one or more input
model files created by previous PROC NLP steps using the
OUTMODEL= option. If it is necessary to include the program code at
a special location in newly written code, the INCLUDE
statement can be used instead of using the MODEL= option.
Using both the
MODEL= option and the INCLUDE statement
with the same model
file will include the same model twice, which can produce
different results than including it once. The MODEL= option
is similar to the option used in PROC MODEL in SAS/ETS software.
-
MSINGULAR=r>0
- MSING=r>0
-
specifies a relative singularity
criterion for measuring singularity of Hessian and
crossproduct Jacobian and their projected forms.
The default value is 1e-12 if
the SINGULAR= option is not specified and
 1e-4* SINGULAR otherwise.
For more information, see the section "Covariance Matrix".
1e-4* SINGULAR otherwise.
For more information, see the section "Covariance Matrix".
-
NOEIGNUM
-
suppresses the computation and
output of the determinant and the inertia of the Hessian,
crossproduct Jacobian, and covariance matrices. The inertia
of a symmetric matrix are the numbers of negative, positive,
and zero eigenvalues. For large applications, the NOEIGNUM
option can save computer time.
-
NOMISS
-
is valid only for those variables
of the DATA= data set that are referred to in program
statements. If the NOMISS option is specified, observations with any
missing value for those variables are skipped. If the NOMISS option
is not specified, the missing value may result in a
missing value of the objective function, implying that
the corresponding BY group of data is not processed.
-
NOPRINT
- NOP
-
suppresses the output.
-
OPTCHECK [=r]
-
computes the function values f(xl) of a grid of
points xl in a small neighborhood of x*.
The xl are located in a ball of radius of r about x*.
If the OPTCHECK optioin is specified without r, the default value is
r=0.1 at the starting point
and r=0.01 at terminating point.
If a point xl* is found with a better function value than
f(x*), then optimization is restarted at xl*.
For more information on grids, see the section "DECVAR Statement".
-
OUT=SAS-data-set
-
creates an output data set that
contains those variables of a DATA= input data set
referred to in the program statements plus additional
variables computed by performing the program statements
of the objective function, derivatives, and nonlinear
constraints. The OUT= data set can also contain
first- and second-order derivatives of these variables
if the OUTDER= option is specified. The variables and
derivatives are evaluated at x*; for TECH=NONE, they are evaluated at x0.
-
OUTALL
-
if an OUTEST= data set is
specified, this option sets the OUTHESSIAN option if the MIN
or MAX statement is used. If the LSQ statement is used, the
OUTALL option sets the OUTCRPJAC option. If nonlinear
constraints are specified using the NLINCON statement, the
OUTALL option sets the OUTNLCJAC option.
-
OUTCRPJAC
-
if an OUTVAR= data set is
specified, the crossproduct Jacobian matrix of the m
functions composing the least-squares function
is written to the OUTVAR= data set.
-
OUTDER= 0, 1, 2
-
specifies whether or not derivatives are
written to the OUT= data set. For OUTDER=2, first-
and second-order derivatives are written to the data set;
for OUTDER=1, only first-order derivatives are written;
for OUTDER=0, no derivatives are written to the data set.
The default value is OUTDER=0. Derivatives are
evaluated at x*.
-
OUTVAR=SAS-data-set
- OUTEST=SAS-data-set
-
creates an output data set that contains the results of the
optimization.
This is useful for reporting and for restarting the optimzation
in a subsequent execution of the procedure.
Information in the data set can include parameter estimates,
gradient values, constraint information, Lagrangian values,
Hessian values, Jacobian values, covariance, standard errors,
and confidence intervals.
-
OUTGRID
-
writes the grid points and their
function values to the OUTEST= data set.
By default, only the feasible grid points points are saved;
however, if the INFEASIBLE option is specified, all
feasible and infeasible grid points are saved.
Note that the BEST= option does not affect the
output of grid points to the OUTEST= or OUTVAR= data set.
For more information on grids, see the section "DECVAR Statement".
-
OUTHESSIAN
- OUTHES
-
writes the
Hessian matrix of the objective function to the OUTEST= data set.
If the Hessian matrix is computed for some other reason
(if, for example, the PHESSIAN option is specified),
the OUTHESSIAN option is set by default.
-
OUTITER
-
during each iteration writes the parameter estimates,
the value of the objective function, the gradient (if available),
and (if OUTTIME is specified) the time in seconds
from the start of the optimization to the OUTEST=
or OUTVAR= data set.
-
OUTJAC
-
writes the Jacobian matrix of the m
functions composing the least-squares function to
the OUTEST= or OUTVAR= data set.
If the PJAC option is specified, the OUTJAC option is set by default.
-
OUTMODEL=model-name
- OUTMOD=model-name
- OUTM=model-name
-
the name of an output model file to which
the program statements are to be written. The program statements
of this file can be included into the program statements of a
succeeding PROC NLP run using the MODEL= option or the INCLUDE
program statement. The OUTMODEL= option is similar to the option
used in PROC MODEL in SAS/ETS software.
Note that the following statements are not part of the
program code that is written to an OUTMODEL= data set:
MIN, MAX, LSQ, MINQUAD, MAXQUAD, PARMS, BOUNDS, BY,
CRPJAC, GRADIENT, HESSIAN, JACNLC, JACOBIAN, LABEL,
LINCON, MATRIX, NLINCON.
-
OUTNLCJAC
-
if an OUTEST= or OUTVAR= data set is
specified, the Jacobian matrix of the nonlinear constraint
functions specified by the NLINCON statement is written to the
OUTEST= data set. If the Jacobian matrix of the nonlinear
constraint functions is computed for some other reason (if,
for example, the PNLCJAC option is specified), the OUTNLCJAC
option is set by default.
-
OUTTIME
-
if an OUTEST= or OUTVAR= data set is
specified and if the OUTITER option is specified, during each
iteration, the time in seconds from the start of the optimization
is written to the OUTEST= or OUTVAR= data set.
-
PALL
- ALL
-
displays all optional output
except the output generated by the
PSTDERR
, PCOV
, LIST
,
or LISTCODE
option.
-
PCOV
-
diplays the covariance matrix specified by the
COV= option. The PCOV option is set automatically if the PALL
and COV= options are set.
-
PCRPJAC
- PJTJ
-
diplays the n ×n
crossproduct Jacobian matrix JTJ. If the PALL option is
specified and the LSQ statement is used, this option is set
automatically. If general linear constraints are active at the
solution, the projected crossproduct Jacobian matrix is also
displayed.
-
PEIGVAL
-
diplays the distribution of eigenvalues
if a G4 inverse is computed for the covariance matrix.
The PEIGVAL option is useful for observing which
eigenvalues of the matrix are recognized as zero eigenvalues
when the generalized inverse is computed, and it is the basis for
setting the COVSING= option in a subsequent execution of PROC NLP.
For more information, see the section "Covariance Matrix"
-
PERROR
-
the PERROR option specifies additional
output for such applications where the program code
for objective function or nonlinear constraints cannot be
evaluated during the iteration process. The PERROR option
is set by default during the evaluations at the starting
point but not during the optimization process.
-
PFUNCTION
-
diplays the values of all functions
specified in a LSQ, MIN, or MAX statement for each observation
read fom the DATA= input data set. The PALL option sets the
PFUNCTION option automatically.
-
PGRID
-
diplays the function values from the grid search.
For more information on grids, see the section "DECVAR Statement".
-
PHESSIAN
- PHES
-
diplays the n ×n
Hessian matrix G. If the PALL option is specified and the MIN
or MAX statement is used, this option is set automatically.
If general linear constraints are active at the
solution, the projected Hessian matrix is also displayed.
-
PHISTORY
- PHIS
-
diplays the optimization
history. No optimization history is displayed for TECH=LICOMP.
This output is included in both the default output
and the output specified by the PALL option.
-
PINIT
- PIN
-
diplays the initial values
and derivatives (if available). This output is included
in both the default output and the output specified by the
PALL option.
-
PJACOBI
- PJAC
-
diplays the m ×n
Jacobian matrix J. Because of the memory requirement for large
least-squares problems, this option is not invoked by using the
PALL option.
-
PNLCJAC
-
diplays the Jacobian matrix of nonlinear
constraints specified by the NLINCON statement. The PNLCJAC
option is set automatically if the PALL option is specified.
-
PSHORT
- SHORT
- PSH
-
restricts the amount
of
default output. If PSHORT is
specified, then
- the initial values are not displayed
- the listing of constraints is not displayed
- if there is more than one function in the MIN, MAX, or
LSQ statement, their values are not displayed
- if the GRADCHECK[=DETAIL] option is used, only the test
vector is displayed
-
PSTDERR
- STDERR
- SE
-
standard errors that are
defined as square
roots of the diagonal elements of the covariance matrix.
The t values and probabilities >|t| are displayed together
with the approximate standard errors. The type of covariance
matrix must be specified using the COV= option. The SIGSQ=
option, the VARDEF= option, and the special variables
_NOBS_ and _DF_ defined in the program statements can
be used to define a scalar factor
 of the
covariance matrix and the approximate
standard errors. For more information, see the section "Covariance Matrix".
of the
covariance matrix and the approximate
standard errors. For more information, see the section "Covariance Matrix".
-
PSUMMARY
- SUMMARY
- SUM
-
restricts the amount of default displayed
output to a short form of iteration history and
notes, warnings and errors.
-
PTIME
-
specifies the output of four different
but partially overlapping differences of CPU time:
- total running time
- total time for the evaluation of objective
function, nonlinear constraints, and derivatives:
shows the total time spent executing
the programming statements specifying the objective
function, derivatives, and nonlinear constraints, and
(if necessary) their firs-t and second-order derivatives.
This is the total of the time needed for code evaluation
before, during, and after iterating
- total time for optimization
shows the total time spent iterating.
- time for some CMP parsing: shows the time needed
for parsing the program statements and its derivatives.
In most applications this is a negligible number, but for
applications that contain ARRAY statements or DO loops
or use an optimization technique with analytic second-order
derivatives, it can be a considerable.
-
RANDOM=i
-
specifies a positive integer as a seed value
for the pseudorandom number generator. Pseudorandom numbers are
used as initial value x(0).
For more information, see the section "PROC NLP Statement".
-
RESTART=i>0
- REST=i>0
-
specifies that
the QUANEW, HYQUAN, or CONGRA algorithm is restarted with
a steepest descent/ascent search direction after at most
i iterations.
Default values are as follows:
- CONGRA: UPDATE=PB: restart is done automatically so
specification of i is not used.
- CONGRA: UPDATE
 PB: i = min(10n,80),
where n is the number of parameters.
PB: i = min(10n,80),
where n is the number of parameters.
- QUANEW, HYQUAN: i is the largest integer available.
-
SIGSQ=sq >0
-
specifies a scalar factor
 for
computing the covariance matrix.
If the
SIGSQ= option is specified, VARDEF=N is the default.
For more information, see the section "Covariance Matrix".
for
computing the covariance matrix.
If the
SIGSQ= option is specified, VARDEF=N is the default.
For more information, see the section "Covariance Matrix".
-
SINGULAR=r > 0
- SING=r > 0
-
specifies the
singularity criterion r for the inversion of the
Hessian matrix and crossproduct Jacobian. The default value
is 1e-8.
See the MSINGULAR= and the VSINGULAR= options in the section "PROC NLP Statement".
-
TECHNIQUE=x
- TECH=x
-
specifies the optimization technique. Valid values for it are as follows:
- CONGRA
chooses one of four
different
conjugate-gradient
optimization algorithms, which can be more precisely specified
with the UPDATE= option and modified with the LINESEARCH= option.
When this option is selected,
UPDATE=PB by default.
For  , CONGRA is the default
optimization technique.
, CONGRA is the default
optimization technique.
- DBLDOG
performs a version of
double dogleg optimization,
which can be more precisely specified
with the UPDATE= option.
When this option is selected,
UPDATE=DBFGS by default.
- HYQUAN
chooses one of three
different hybrid quasi-Newton
optimization algorithms which can be more precisely defined
with the VERSION= option and modified with the LINESEARCH=
option.
By default,VERSION=2 and UPDATE=DBFGS.
- LM
performs the Levenberg-Marquardt
minimization.
For n < 40, this is the default minimization
technique for least-squares problems.
- LCP
solves a quadratic program as a linear complementarity problem.
- NMSIMP
performs the Nelder-Mead
simplex
optimization method.
- NONE
does not perform any
optimization. This option can be used
- to do grid search without optimization
- to compute and display derivatives and covariance
matrices which cannot be obtained efficiently with any
of the optimization techniques
- NEWRAP
performs the Newton-Raphson
optimization technique.
The algorithm combines a line-search algorithm with ridging.
The line-search algorithm LIS=2 is the default.
- NRRIDG
performs the Newton-Raphson
optimization technique. For  and non-linear least-squares, this is the default.
and non-linear least-squares, this is the default.
- QUADAS
performs a special
quadratic version of the active set strategy.
- QUANEW
chooses one of four
quasi-Newton
optimization algorithms
which can be defined more precisely with the UPDATE= option
and modified with the LINESEARCH= option.
This is the default for 40 < n < 400 or
if there are nonlinear constraints.
- TRUREG
performs the trust region
optimization technique.
-
m
- UPD=m
-
specifies the update
method for the (dual) quasi-Newton, double dogleg, hybrid
quasi-Newton, or conjugate-gradient optimization technique.
Not every update method can be used with each optimizer.
For more information, see the section "Optimization Algorithms".
Valid values for m are as follows:
- BFGS
-
performs the original BFGS
(Broyden, Fletcher,
Goldfarb, & Shanno) update of the inverse Hessian matrix.
- DBFGS
-
performs the dual BFGS
(Broyden, Fletcher, Goldfarb, & Shanno)
update of the Cholesky factor of the Hessian matrix.
- DDFP
-
performs the dual DFP
(Davidon, Fletcher, & Powell)
update of the Cholesky factor of the Hessian matrix.
- DFP
-
performs the original DFP
(Davidon, Fletcher, & Powell)
update of the inverse Hessian matrix.
- PB
-
performs the automatic restart
update method of
Powell (1977)
and Beale (1972).
- FR
-
performs the
Fletcher-Reeves update (Fletcher 1987).
- PR
-
performs the Polak-Ribiere
update
(Fletcher 1987).
- CD
-
performs a
conjugate-descent update of
Fletcher (1987).
-
VARDEF=DF,N
-
specifies the divisor d used in the
calculation of the covariance matrix and approximate standard
errors.
If the SIGSQ= option is not specified, the default value is
VARDEF= DF; otherwise, VARDEF=N is default.
For more information, see the section "Covariance Matrix".
-
VERSION=1, 2, 3
- VS=1, 2, 3
-
zx
specifies the version
of the hybrid quasi-Newton
optimization
technique or the version of the quasi-Newton optimization
technique with nonlinear constraints.
For hybrid quasi-Newton optimization technique
- VS=1
- specifies version HY1 of Fletcher & Xu (1987)
- VS=2
- specifies version HY2 of Fletcher & Xu (1987)
- VS=3
- specifies version HY3 of Fletcher & Xu (1987)
For quasi-Newton optimization technique with nonlinear
constraints,
- VS=1
- specifies the update of the
 vector
like Powell (1978)
(update like VF02AD)
vector
like Powell (1978)
(update like VF02AD)
- VS=2
- specifies the update of the
 vector
like Powell (1982) (update like VMCWD)
vector
like Powell (1982) (update like VMCWD)
In both cases, the default value is VS=2.
-
VSINGULAR=r>0
- VSING=r>0
-
specifies a relative singularity
criterion
for measuring singularity
of Hessian and crossproduct Jacobian and their projected
forms, which may have to be converted to compute the
covariance matrix. The default value for VSING is 1e-8 if
the SINGULAR= option is not specified and the value of
SINGULAR otherwise.
For more information, see the section "Covariance Matrix".
-
XCONV=r[n]
- XTOL=r[n]
-
specifies the relative
parameter convergence criterion. For all techniques except
NMSIMP, termination requires a small relative parameter change
in subsequent iterations,
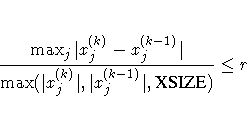
For the NMSIMP technique, the same formula is used, but
xj(k) is defined as the vertex with the lowest function
value and xj(k-1) is defined as the vertex with the highest
function value in the simplex. The default value is r=1e-8 for
the NMSIMP technique and r=0 otherwise.
The optional integer value n specifies the number of successive
iterations for which the criterion must be satisfied before the
process can be terminated.
-
XSIZE=r>0
-
specifies the XSIZE parameter of the relative
parameter termination criterion. The default value is r=0.
For more detail, see the XCONV= option in the section "PROC NLP Statement".
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
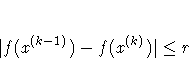
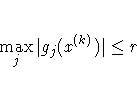
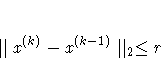
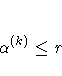
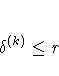
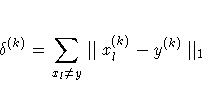
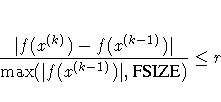
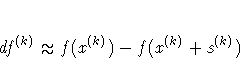
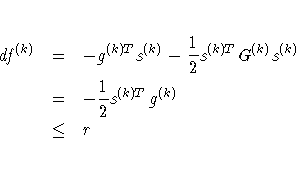
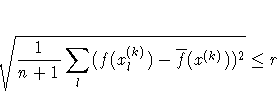
![{ g(x^{(k)})^T [G^{(k)}]^{-1} g(x^{(k)}) \over
\max(| f(x^{(k)})|,{FSIZE}) } \leq r](images/nlpeq32.gif)