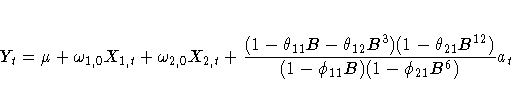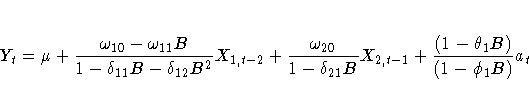OUTEST= Data Set

The ARIMA Procedure

OUTEST= Data Set

PROC ARIMA writes the parameter estimates for a model to an output data set when the OUTEST= option is specified in the ESTIMATE statement. The OUTEST= data set contains the following:

the BY variables
_NAME_, a character variable containing the name of the parameter for the covariance or correlation observations, or blank for the observations containing the parameter estimates. (This variable is not created if neither OUTCOV nor OUTCORR is specified.)
_TYPE_, a character variable that identifies the type of observation. A description of the _TYPE_ variable values is given below.
variables for model parameters

The variables for the model parameters are named as follows:

ERRORVAR: This numeric variable contains the variance estimate. The _TYPE_=EST observation for this variable contains the estimated error variance, and the remaining observations are missing.
MU: This numeric variable contains values for the mean parameter for the model. (This variable is not created if NOCONSTANT is specified.)
MAj_k: These numeric variables contain values for the moving average parameters. The variables for moving average parameters are named MAj_k, where j is the factor number, and k is the index of the parameter within a factor.
ARj_k: These numeric variables contain values for the autoregressive parameters. The variables for autoregressive parameters are named ARj_k, where j is the factor number, and k is the index of the parameter within a factor.
Ij_k: These variables contain values for the transfer function parameters. Variables for transfer function parameters are named Ij_k, where j is the number of the INPUT variable associated with the transfer function component, and k is the number of the parameter for the particular INPUT variable. INPUT variables are numbered according to the order in which they appear in the INPUT= list.
_STATUS_: This variable describes the convergence status of the model. A value of 0_CONVERGED indicates that the model converged.

The value of the _TYPE_ variable for each observation indicates the kind of value contained in the variables for model parameters for the observation. The OUTEST= data set contains observations with the following _TYPE_ values:

EST: the observation contains parameter estimates
STD: the observation contains approximate standard errors of the estimates
CORR: the observation contains correlations of the estimates. OUTCORR must be specified to get these observations.
COV: the observation contains covariances of the estimates. OUTCOV must be specified to get these observations.
FACTOR: the observation contains values that identify for each parameter the factor that contains it. Negative values indicate denominator factors in transfer function models.
LAG: the observation contains values that identify the lag associated with each parameter
SHIFT: the observation contains values that identify the shift associated with the input series for the parameter

The values given for _TYPE_=FACTOR, _TYPE_=LAG, or _TYPE_=SHIFT observations enable you to reconstruct the model employed when provided with only the OUTEST= data set.

OUTEST= Examples

This section clarifies how model parameters are stored in the OUTEST= data set with two examples.

Consider the following example:


   proc arima data=input;
      identify var=y cross=(x1 x2);
      estimate p=(1)(6) q=(1,3)(12) input=(x1 x2) outest=est;
   quit;
   proc print data=est;
   run;

The model specified by these statements is

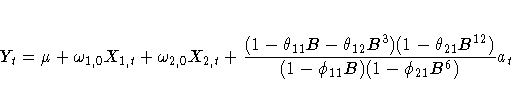
$Y_{t}={\mu}+{\omega}_{1,0}X_{1,t}+{\omega}_{2,0}X_{2,t} + \frac{(1-{\theta}_{11... ...eta}_{12}B^3)(1-{\theta}_{21}B^{12})}{(1-{\phi}_{11}B)(1-{\phi}_{21}B^6)} a_{t}$

The OUTEST= data set contains the values shown in Table 7.9.

Table 7.9: OUTEST= Data Set for First Example

Obs	_TYPE_	Y	MU	MA1_1	MA1_2	MA2_1	AR1_1	AR2_1	I1_1	I2_1
1	EST	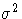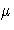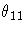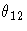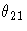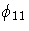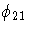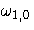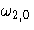${{\sigma}^2}$	${\mu}$	${{\theta}_{11}}$	${{\theta}_{12}}$	${{\theta}_{21}}$	${{\phi}_{11}}$	${{\phi}_{21}}$	${{\omega}_{1,0}}$	${{\omega}_{2,0}}$
2	STD	.	se 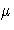${\mu}$	se 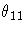${{\theta}_{11}}$	se 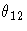${{\theta}_{12}}$	se 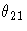${{\theta}_{21}}$	se 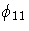${{\phi}_{11}}$	se 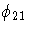${{\phi}_{21}}$	se 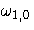${{\omega}_{1,0}}$	se 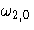${{\omega}_{2,0}}$
3	FACTOR	.	0	1	1	2	1	2	1	1
4	LAG	.	0	1	3	12	1	6	0	0
5	SHIFT	.	0	0	0	0	0	0	0	0

Note that the symbols in the rows for _TYPE_=EST and _TYPE_=STD in Table 7.9 would be numeric values in a real data set.

Next, consider the following example:


   proc arima data=input;
      identify var=y cross=(x1(2) x2(1));
      estimate p=1 q=1 input=(2 $ (1)/(1,2)x1 1 $ /(1)x2) outest=est;
   quit;
   proc print data=est;
   run;

The model specified by these statements is

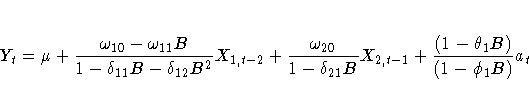
$Y_{t}={\mu}+\frac{{\omega}_{10}-{\omega}_{11}B}{1-{\delta}_{11}B -{\delta}_{12}... ...0}}{1-{\delta}_{21}B}X_{2,t-1} +\frac{(1-{\theta}_{1}B)}{(1-{\phi}_{1}B)}a_{t}$

The OUTEST= data set contains the values shown in Table 7.10.

Table 7.10: OUTEST= Data Set for Second Example

Obs	_TYPE_	Y	MU	MA1_1	AR1_1	I1_1	I1_2	I1_3	I1_4	I2_1	I2_2
1	EST	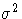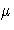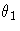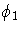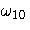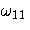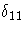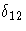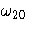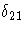${{\sigma}^2}$	${\mu}$	${{\theta}_{1}}$	${\phi}_{1}$	${{\omega}_{10}}$	${{\omega}_{11}}$	${{\delta}_{11}}$	${{\delta}_{12}}$	${{\omega}_{20}}$	${{\delta}_{21}}$
2	STD	.	se 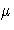${\mu}$	se 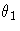${{\theta}_{1}}$	se 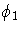${\phi}_{1}$	se 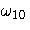${{\omega}_{10}}$	se 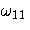${{\omega}_{11}}$	se 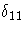${{\delta}_{11}}$	se 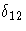${{\delta}_{12}}$	se 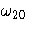${{\omega}_{20}}$	se 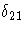${{\delta}_{21}}$
3	FACTOR	.	0	1	1	1	1	-1	-1	1	-1
4	LAG	.	0	1	1	0	1	1	2	0	1
5	SHIFT	.	0	0	0	2	2	2	2	1	1

Chapter Contents
Previous
Next
Top