The MINIC Method

The ARIMA Procedure

The MINIC Method

The MINimum Information Criterion (MINIC) method can tentatively identify the order of a stationary and invertible ARMA process. Note that Hannan and Rissannen (1982) proposed this method, and Box et al (1994) and Choi (1990) provide useful descriptions of the algorithm.

Given a stationary and invertible time series ${\{z_{t} : 1 \leq t \leq n\} }$ with mean corrected form ${\tilde{z}_{t} = z_{t} - {\mu}_{z}}$ , with a true autoregressive order of p, and with a true moving-average order of q, you can use the MINIC method to compute information criteria (or penalty functions) for various autoregressive and moving average orders. The following paragraphs provide a brief description of the algorithm.

If the series is a stationary and invertible ARMA(p,q) process of the form

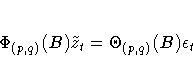
${\Phi}_{(p,q)}( B)\tilde{z}_{t} = {\Theta}_{(p,q)}(B){\epsilon}_{t}$

the error series can be approximated by a high-order AR process

$\hat{{\epsilon}}_{t} = \hat{{\Phi}}_{(p_{{\epsilon}},q)}(B)\tilde{z}_{t} \approx {\epsilon}_{t}$

where the parameter estimates ${\hat{{\Phi}}_{(p_{{\epsilon}},q)}}$ are obtained from the Yule-Walker estimates. The choice of the autoregressive order, ${p_{{\epsilon}}}$ , is determined by the order that minimizes the Akaike information criterion (AIC) in the range ${p_{{\epsilon},min} \leq p_{{\epsilon}} \leq p_{{\epsilon},max} }$

${AIC}(p_{{\epsilon}},0) = {\rm ln} ( \tilde{{\sigma}}^2_{(p_{{\epsilon}},0)} ) + 2 ( p_{{\epsilon}} + 0 ) / n$

where

$\tilde{{\sigma}}^2_{(p_{{\epsilon}},0)} = \frac{1}n\sum_{t=p_{{\epsilon}}+1}^n \hat{{\epsilon}}^2_{t}$

Note that Hannan and Rissannen (1982) use the Bayesian information criterion (BIC) to determine the autoregressive order used to estimate the error series. Box et al (1994) and Choi (1990) recommend the AIC.

Once the error series has been estimated for autoregressive test order m = p_min, ... , p_max and for moving-average test order j = q_min, ... , q_max, the OLS estimates ${\hat{{\Phi}}_{(m,j)}}$ and ${\hat{{\Theta}}_{(m,j)}}$ are computed from the regression model

$\tilde{z}_{t} = \sum_{i=1}^m {\phi}^{(m,j)}_{i} \tilde{z}_{t-i} + \sum_{k=1}^j {\theta}^{(m,j)}_{k}\hat{{\epsilon}}_{t-k} + error$

From the preceding parameter estimates, the BIC is then computed

${BIC}(m,j) = {\rm ln}( \tilde{{\sigma}}^2_{(m,j)} ) + 2(m+j){\rm ln}(n)/n$

where

$\tilde{\sigma}^2_{(m,j)} = \frac{1}n \sum_{t=t_0}^n ( \tilde{z}_t - \sum_{i=... ...,j)} \tilde{z}_{t-i} + \sum_{k=1}^j \theta_k^{(m,j)} \hat{\epsilon}_{t-k} )$

where ${t_{0}=p_{{\epsilon}} + \rm{max}(m,j)}$ .

A MINIC table is then constructed using BIC(m,j) (see Table 7.5). If ${p_{max} \gt p_{{\epsilon},min} }$ , the preceding regression may fail due to linear dependence on the estimated error series and the mean-corrected series. Values of BIC(m,j) that cannot be computed are set to missing. For large autoregressive and moving average test orders with relatively few observations, a nearly perfect fit can result. This condition can be identified by a large negative BIC(m,j) value.

Table 7.5: MINIC Table

	MA
AR	0	1	2	3	·	·
0	BIC(0,0)	BIC(0,1)	BIC(0,2)	BIC(0,3)	·	·
1	BIC(1,0)	BIC(1,1)	BIC(1,2)	BIC(1,3)	·	·
2	BIC(2,0)	BIC(2,1)	BIC(2,2)	BIC(2,3)	·	·
3	BIC(3,0)	BIC(3,1)	BIC(3,2)	BIC(3,3)	·	·
·	·	·	·	·	·	·
·	·	·	·	·	·	·

Chapter Contents
Previous
Next
Top