White Noise Test

The SPECTRA Procedure

White Noise Test

PROC SPECTRA prints two test statistics for white noise when the WHITETEST option is specified: Fisher's Kappa (Davis 1941, Fuller 1976) and Bartlett's Kolmogorov-Smirnov statistic (Bartlett 1966, Fuller 1976, Durbin 1967).

If the time series is a sequence of independent random variables with mean 0 and variance ${{\sigma}^2}$ , then the periodogram, J_k, will have the same expected value for all k. For a time series with nonzero autocorrelation, each ordinate of the periodogram, J_k, will have different expected values. The Fisher's Kappa statistic tests whether the largest J_k can be considered different from the mean of the J_k. Critical values for the Fisher's Kappa test can be found in Fuller 1976 and SAS/ETS Software: Applications Guide 1.

The Kolmogorov-Smirnov statistic reported by PROC SPECTRA has the same asymtotic distribution as Bartlett's test (Durbin 1967). The Kolmogorov-Smirnov statistic compares the normalized cumulative periodogram with the cumulative distribution function of a uniform(0,1) random variable. The normalized cumulative periodogram, F_j, of the series is

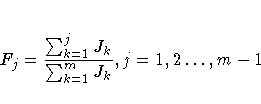
$F_{j} = \frac{\sum_{k=1}^j{J_{k}}}{\sum_{k=1}^m{J_{k}}}, j = 1, 2 ... , m-1$

where m = [n/2] if n is even or m = [(n-1)/2] if n is odd. The test statistic is the maximum absolute difference of the normalized cumulative periodogram and the uniform cumulative distribution function. For m-1 greater than 100, if Bartlett's Kolmogorov-Smirnov statistic exceeds the critical value

$\frac{a}{\sqrt{m-1}}$

where a=1.36 or a=1.63 corresponding to 5% or 1% significance levels respectively, then reject the null hypothesis that the series represents white noise. Critical values for m-1 < 100 can be found in a table of significance points of the Kolmogorov-Smirnov statistics with sample size m-1 (Miller 1956, Owen 1962).

Chapter Contents
Previous
Next
Top