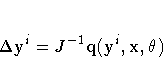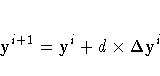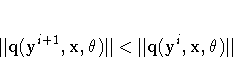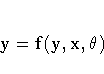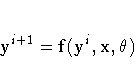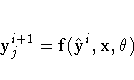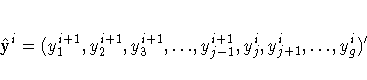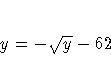Numerical Solution Methods

The MODEL Procedure

Numerical Solution Methods

If the SINGLE option is not used, PROC MODEL computes values that simultaneously satisfy the model equations for the variables named in the SOLVE statement. PROC MODEL provides three iterative methods, Newton, Jacobi, and Seidel, for computing a simultaneous solution of the system of nonlinear equations.

Single-Equation Solution

For normalized-form equation systems, the solution can either simultaneously satisfy all the equations or can be computed for each equation separately, using the actual values of the solution variables in the current period to compute each predicted value. By default, PROC MODEL computes a simultaneous solution. The SINGLE option on the SOLVE statement selects single-equation solutions.

Single-equation simulations are often made to produce residuals (which estimate the random terms of the stochastic equations) rather than the predicted values themselves. If the input data and range are the same as that used for parameter estimation, a static single-equation simulation will reproduce the residuals of the estimation.

Newton's Method

The NEWTON option on the SOLVE statement requests Newton's method to simultaneously solve the equations for each observation. Newton's method is the default solution method. Newton's method is an iterative scheme that uses the derivatives of the equations with respect to the solution variables, J, to compute a change vector as

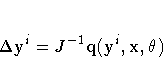
${\Delta} y^i = J^{-1}q(y^i,x, {{\theta}})$

PROC MODEL builds and solves J using efficient sparse matrix techniques. The solution variables yⁱ at the ith iteration are then updated as

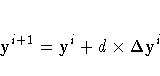
$y^{i+1} = y^i + d x {\Delta} y^i$

d is a damping factor between 0 and 1 chosen iteratively so that

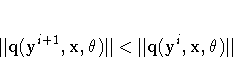
${\Vert} q(y^{i+1},x, {{\theta}}) {\Vert} \lt {\Vert} q(y^i,x, {{\theta}}) {\Vert}$

The number of subiterations allowed for finding a suitable d is controlled by the MAXSUBITER= option. The number of iterations of Newton's method allowed for each observation is controlled by MAXITER= option. Refer to Ortega and Rheinbolt (1970) for more details.

Jacobi Method

The JACOBI option on the SOLVE statement selects a matrix-free alternative to Newton's method. This method is the traditional nonlinear Jacobi method found in the literature. The Jacobi method as implemented in PROC MODEL substitutes predicted values for the endogenous variables and iterates until a fixed point is reached. Then necessary derivatives are computed only for the diagonal elements of the jacobian, J.

If the normalized-form equation is

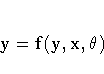
$y = f(y,x, {{\theta}})$

the Jacobi iteration has the form

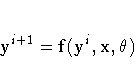
$y^{i+1} = f(y^i,x, {{\theta}})$

Seidel Method

The Seidel method is an order-dependent alternative to the Jacobi method. The Seidel method is selected by the SEIDEL option on the SOLVE statement and is applicable only to normalized-form equations. The Seidel method is like the Jacobi method except that in the Seidel method the model is further edited to substitute the predicted values into the solution variables immediately after they are computed. Seidel thus differs from the other methods in that the values of the solution variables are not fixed within an iteration. With the other methods, the order of the equations in the model program makes no difference, but the Seidel method may work much differently when the equations are specified in a different sequence. Note that this fixed point method is the traditional nonlinear Seidel method found in the literature.

The iteration has the form

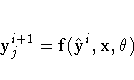
$y^{i+1}_{j} = f({\hat{y}}^i,x, {{\theta}})$

where yⁱ⁺¹_j is the jth equation variable at the ith iteration and

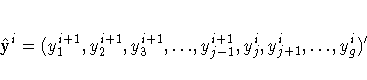
${\hat{y}}^i = ( y^{i+1}_{1}, y^{i+1}_{2}, y^{i+1}_{3}, { ... }, y^{i+1}_{j-1}, y^i_{j}, y^i_{j+1}, { ... }, y^i_{g})'$

If the model is recursive, and if the equations are in recursive order, the Seidel method will converge at once. If the model is block-recursive, the Seidel method may converge faster if the equations are grouped by block and the blocks are placed in block-recursive order. The BLOCK option can be used to determine the block-recursive form.

Comparison of Methods

Newton's method is the default and should work better than the others for most small- to medium-sized models. The Seidel method is always faster than the Jacobi for recursive models with equations in recursive order. For very large models and some highly nonlinear smaller models, the Jacobi or Seidel methods can sometimes be faster. Newton's method uses more memory than the Jacobi or Seidel methods.

Both the Newton's method and the Jacobi method are order-invariant in the sense that the order in which equations are specified in the model program has no effect on the operation of the iterative solution process. In order-invariant methods, the values of the solution variables are fixed for the entire execution of the model program. Assignments to model variables are automatically changed to assignments to corresponding equation variables. Only after the model program has completed execution are the results used to compute the new solution values for the next iteration.

Troubleshooting Problems

In solving a simultaneous nonlinear dynamic model you may encounter some of the following problems.

[cmodelfsolvemi]Missing Values For SOLVE tasks, there can be no missing parameter values. If there are missing right-hand-side variables, this will result in a missing left-hand-side variable for that observation.

Unstable Solutions

A solution may exist but be unstable. An unstable system can cause the Jacobi and Seidel methods to diverge.

Explosive Dynamic Systems

A model may have well-behaved solutions at each observation but be dynamically unstable. The solution may oscillate wildly or grow rapidly with time.

Propagation of Errors

During the solution process, solution variables can take on values that cause computational errors. For example, a solution variable that appears in a LOG function may be positive at the solution but may be given a negative value during one of the iterations. When computational errors occur, missing values are generated and propagated, and the solution process may collapse.

Convergence Problems

The following items can cause convergence problems:

illegal function values ( that is ${\sqrt{-1}}$ )
local minima in the model equation
no solution exists
multiple solutions exist
initial values too far from the solution
the CONVERGE= value too small.

When PROC MODEL fails to find a solution to the system, the current iteration information and the program data vector are printed. The simulation halts if actual values are not available for the simulation to proceed. Consider the following program:

   data test1;
      do t=1 to 50;
         x1 = sqrt(t) ;
         y = .;
         output;
      end;
   
   proc model data=test1;
      exogenous x1 ;
      control a1 -1 b1 -29 c1 -4 ;
      y = a1 * sqrt(y) + b1 * x1 * x1 + c1 * lag(x1);
      solve y / out=sim forecast dynamic ;
   run;

which produces the output shown in Figure 14.70.

The MODEL Procedure

Dynamic Single-Equation Forecast

ERROR: Could not reduce norm of residuals in 10 subiterations.

ERROR: The solution failed because 1 equations are missing or have extreme values for observation 1 at NEWTON iteration 1.

NOTE: Additional information on the values of the variables at this observation, which may be helpful in determining the cause of the failure of the solution process, is printed below.

Observation	1	Iteration	1	CC	-1.000000
		Missing	1

Iteration Errors - Missing.

_N_: 12 ACTUAL.x1: 1.41421 ACTUAL.y: . ERROR.y: . PRED.y: . RESID.y: . a1: -1 b1: -29 c1: -4 x1: 1.41421 y: -0.00109 @PRED.y/@y: . @ERROR.y/@y: .

Observation	1	Iteration	1	CC	-1.000000
		Missing	1

ERROR: 1 execution errors for this observation

NOTE: Check for missing input data or uninitialized lags.

(Note that the LAG and DIF functions return missing values for the initial lag starting observations. This is a change from the 1982 and earlier versions of SAS/ETS which returned zero for uninitialized lags.)

NOTE: Simulation aborted.

Figure 14.70: SOLVE Convergence Problems

At the first observation the following equation is attempted to be solved:

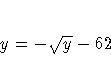
$y = - \sqrt{y} - 62$

There is no solution to this problem. The iterative solution process got as close as it could to making Y negative while still being able to evaluate the model. This problem can be avoided in this case by altering the equation.

In other models, the problem of missing values can be avoided by either altering the data set to provide better starting values for the solution variables or by altering the equations.

You should be aware that, in general, a nonlinear system can have any number of solutions, and the solution found may not be the one that you want. When multiple solutions exist, the solution that is found is usually determined by the starting values for the iterations. If the value from the input data set for a solution variable is missing, the starting value for it is taken from the solution of the last period (if nonmissing) or else the solution estimate is started at 0.

Iteration Output

The iteration output, produced by the ITPRINT option, is useful in determining the cause of a convergence problem. The ITPRINT option forces the printing of the solution approximation and equation errors at each iteration for each observation. A portion of the ITPRINT output from

   proc model data=test1;
      exogenous x1 ;
      control a1 -1 b1 -29 c1 -4 ;
      y = a1 * sqrt(abs(y)) + b1 * x1 * x1 + c1 * lag(x1);
      solve y / out=sim forecast dynamic itprint;
   run;

is shown in Figure 14.71.

The MODEL Procedure

Dynamic Single-Equation Forecast

Observation	1	Iteration	0	CC	613961.39	ERROR.y	-62.01010

Predicted Values
y
0.0001000

Iteration Errors
y
-62.01010

Observation	1	Iteration	1	CC	50.902771	ERROR.y	-61.88684

Predicted Values
y
-1.215784

Iteration Errors
y
-61.88684

Observation	1	Iteration	2	CC	0.364806	ERROR.y	41.752112

Predicted Values
y
-114.4503

Iteration Errors
y
41.75211

Figure 14.71: SOLVE, ITPRINT Output

For each iteration, the equation with the largest error is listed in parentheses after the Newton convergence criteria measure. From this output you can determine which equation or equations in the system are not converging well.

Chapter Contents
Previous
Next
Top