Estimation Methods

The MODEL Procedure

Estimation Methods

Consider the general nonlinear model:

${{\epsilon}}_{t}\hspace*{2pt} &=& q(y_{t}\hspace*{1pt}, x_{t}\hspace*{1pt}, {{\theta}}) \cr z_{t} &=& Z(x_{t})\hspace*{2pt}$

where q ${\in}{ R^g}$ is a real vector valued function, of y_t ${\in}{ R^g}$ , x_t ${\in} { R^l}$ , ${\theta}$ ${\in}{ R^p}$ , g is the number of equations, l is the number of exogenous variables (lagged endogenous variables are considered exogenous here), p is the number of parameters and t ranges from 1 to n. z_t ${\in}R^k$ is a vector of instruments. ${\epsilon}$ _t is an unobservable disturbance vector with the following properties:

$E({{\epsilon}}_{t}) &=& 0 \cr E({{\epsilon}}_{t} {{\epsilon}}^{'}_{t} ) &=& {\Sigma}$

All of the methods implemented in PROC MODEL aim to minimize an objective function. The following table summarizes the objective functions defining the estimators and the corresponding estimator of the covariance of the parameter estimates for each method.

Table 14.1: Summary of PROC MODEL Estimation Methods

Method	Instruments	Objective Function	Covariance of ${\theta}$
OLS	no	r'r/n	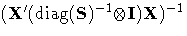${( X'(\rm{diag}(S)^{-1} {\otimes} I)X)^{-1}}$
ITOLS	no	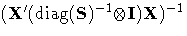${r'(\rm{diag}(S)^{-1} {\otimes} I)r/n}$	${( X'(\rm{diag}(S)^{-1} {\otimes} I)X)^{-1}}$
SUR	no	${r'( S^{-1}_{\rm{OLS}} {\otimes} I)r/n}$	${( X'(S^{-1} {\otimes} I)X)^{-1}}$
ITSUR	no	${r'(S^{-1} {\otimes} I)r/n}$	${( X'(S^{-1} {\otimes} I)X)^{-1}}$
N2SLS	yes	${r'(I {\otimes} W)r/n}$	${( X'(\rm{diag}(S)^{-1} {\otimes} W)X)^{-1}}$
IT2SLS	yes	${r'(\rm{diag}(S)^{-1} {\otimes} W)r/n}$	${( X'(\rm{diag}(S)^{-1} {\otimes} W)X)^{-1}}$
N3SLS	yes	${r'( S^{-1}_{\rm{N2SLS}} {\otimes} W)r/n}$	${( X'(S^{-1} {\otimes} W)X)^{-1}}$
IT3SLS	yes	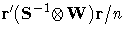${r'(S^{-1} {\otimes} W)r/n}$	${( X'(S^{-1} {\otimes} W)X)^{-1}}$
GMM	yes	${[n{m}_{n}({\theta})]' \hat{V}\hspace*{1pt}^{-1}_{\rm{N2SLS}}[n{m}_{n}({\theta})]}$	${ [(Y{X})'\hat{V}^{-1}(Y{X})]^{-1}}$
ITGMM	yes	${[n{m}_{n}({\theta})]' \hat{V}\hspace*{1pt}^{-1}[n{m}_{n}({\theta})]}$	${ [(Y{X})'\hat{V}^{-1}(Y{X})]^{-1}}$
FIML	no	constant+[n/2]ln(det(S))	${ [\hat{Z} ' ( S ^{-1} {\otimes} I) \hat{Z}]^{-1}}$
		${-\sum_{1}^n{{\ln} \|(J_{t})\| }}$

The column labeled "Instruments" identifies the estimation methods that require instruments. The variables used in this table and the remainder of this chapter are defined as follows:

n = is the number of nonmissing observations.

g = is the number of equations.

k = is the number of instrumental variables.

${{r } = [\matrix{r_{1} \cr r_{2} \cr {\vdots} \cr r_{g}}] }$ is the ng ×1 vector of residuals for the g equations stacked together.

${r_{i} = [\matrix{q_{i}(y_{1}\hspace*{1pt}, x_{1}\hspace*{1pt}, {{\theta}}) \cr ... ...) \cr {\vdots} \cr q_{i}(y_{n}\hspace*{1pt}, x_{n}\hspace*{1pt}, {{\theta}}) }]}$ is the n ×1 column vector of residuals for the ith equation.

S

is a g ×g matrix that estimates ${\Sigma}$ , the covariances of the errors across equations (referred to as the S matrix).

X

is an ng ×p matrix of partial derivatives of the residual with respect to the parameters.

W

is an n ×n matrix, Z(Z'Z)^-1Z'.

Z

is an n ×k matrix of instruments.

Y

is a gk ×ng matrix of instruments. ${Y = I_{g} {\otimes} Z'}$ .

${\hat Z}$

${\hat{Z} = ( \hat{Z}_{1}, \hat{Z}_{2}, { ... },\hat{Z}_{p} )}$ is an ng × p matrix. ${\hat{Z}_{i}}$ is a ng × 1 column vector obtained from stacking the columns of

$U \frac{1}n \sum_{t=1}^n{ ( \frac{\partial q(y _{t}\hspace*{1pt}, x_{t}\hspace... ...t}\hspace*{1pt},{{\theta}})'}{{\partial} y_{t}{\partial} {\theta}_{i}} - Q_{i}$

U

is an n × g matrix of residual errors. ${U = {\ssbeleven {{\epsilon}}_{1}, {{\epsilon}}_{2}, { ... }, {{\epsilon}}_{n}}'}$

Q

is the n × g matrix ${{\ssbeleven q(y _{1}\hspace*{1pt}, x_{1}\hspace*{1pt}, {{\theta}}), q(y _{2}\hs... ...{{\theta}}),{ ... }, q(y _{n}\hspace*{1pt}, x_{n}\hspace*{1pt}, {{\theta}}) } '}$ .

Q_i

is an n × g matrix ${\frac{{\partial}Q}{{\partial} {\theta}_{i}} }$ .

I

is an n ×n identity matrix.

J_t

is ${\frac{{\partial} q(y_{t}\hspace*{1pt}, x_{t}\hspace*{1pt}, {{\theta}})}{{\partial}y_{t}^{'}}}$ which is a g ×g Jacobian matrix.

m_n

is first moment of the crossproduct ${q(y_{t}, x_{t}, {{\theta}}) {\otimes} z_{t}}$ .

${m_{n}=\frac{1}n \sum_{t=1}^n{q(y_{t}\hspace*{1pt}, x_{t}\hspace*{1pt}, {{\theta}}) {\otimes} z_{t}}}$

z_t

is a k column vector of instruments for observation t. z'_t is also the tth row of Z.

${\hat{V}}$

is the gk ×gk matrix representing the variance of the moment functions.

k

is the number of instrumental variables used.

constant

is the constant ${\frac{ng}2 (1 + {\ln}( 2 {\pi} ))}$ .

${\otimes}$

is the notation for a Kronecker product.

All vectors are column vectors unless otherwise noted. Other estimates of the covariance matrix for FIML are also available.

Dependent Regressors and Two-Stage Least Squares

Ordinary regression analysis is based on several assumptions. A key assumption is that the independent variables are in fact statistically independent of the unobserved error component of the model. If this assumption is not true--if the regressor varies systematically with the error--then ordinary regression produces inconsistent results. The parameter estimates are biased.

Regressors might fail to be independent variables because they are dependent variables in a larger simultaneous system. For this reason, the problem of dependent regressors is often called simultaneous equation bias. For example, consider the following two-equation system.

$y_{1} = a_{1} + b_{1} y_{2} + c_{1} x_{1} + {\epsilon}_{1}$

$y_{2} = a_{2} + b_{2} y_{1} + c_{2} x_{2} + {\epsilon}_{2}$

In the first equation, y₂ is a dependent, or endogenous, variable. As shown by the second equation, y₂ is a function of y₁, which by the first equation is a function of ${\epsilon}$ ₁, and therefore y₂ depends on ${\epsilon}$ ₁. Likewise, y₁ depends on ${\epsilon}$ ₂ and is a dependent regressor in the second equation. This is an example of a simultaneous equation system; y₁ and y₂ are a function of all the variables in the system.

Using the ordinary least squares (OLS) estimation method to estimate these equations produces biased estimates. One solution to this problem is to replace y₁ and y₂ on the right-hand side of the equations with predicted values, thus changing the regression problem to the following:

$y_{1} = a_{1} + b_{1} \hat{y}_{2} + c_{1} x_{1} + {\epsilon}_{1}$

$y_{2} = a_{2} + b_{2} \hat{y}_{1} + c_{2} x_{2} + {\epsilon}_{2}$

This method requires estimating the predicted values ${\hat{y}_{1}}$ and ${\hat{y}_{2}}$ through a preliminary, or "first stage," instrumental regression. An instrumental regression is a regression of the dependent regressors on a set of instrumental variables, which can be any independent variables useful for predicting the dependent regressors. In this example, the equations are linear and the exogenous variables for the whole system are known. Thus, the best choice for instruments (of the variables in the model) are the variables x₁ and x₂.

This method is known as two-stage least squares or 2SLS, or more generally as the instrumental variables method. The 2SLS method for linear models is discussed in Pindyck (1981, p. 191-192). For nonlinear models this situation is more complex, but the idea is the same. In nonlinear 2SLS, the derivatives of the model with respect to the parameters are replaced with predicted values. See the section "Choice of Instruments" for further discussion of the use of instrumental variables in nonlinear regression.

To perform nonlinear 2SLS estimation with PROC MODEL, specify the instrumental variables with an INSTRUMENTS statement and specify the 2SLS or N2SLS option on the FIT statement. The following statements show how to estimate the first equation in the preceding example with PROC MODEL.

   proc model data=in;
      y1 = a1 + b1 * y2 + c1 * x1;
      fit y1 / 2sls;
      instruments x1 x2;
   run;

The 2SLS or instrumental variables estimator can be computed using a first-stage regression on the instrumental variables as described previously. However, PROC MODEL actually uses the equivalent but computationally more appropriate technique of projecting the regression problem into the linear space defined by the instruments. Thus PROC MODEL does not produce any "first stage" results when you use 2SLS. If you specify the FSRSQ option on the FIT statement, PROC MODEL prints "first-stage R²" statistic for each parameter estimate.

Formally, the ${\hat{{{\theta}}}}$ that minimizes

$\hspace*{-0.40in}\hat{S}_{n} = \frac{1}n (\sum_{t=1}^n{(q(y_{t}\hspace*{1pt}, ... ...1}^n{(q(y_{t}\hspace*{1pt}, x_{t}\hspace*{1pt},{{\theta}}) {\otimes} z_{t})})$

is the N2SLS estimator of the parameters. The estimate of ${\Sigma}$ at the final iteration is used in the covariance of the parameters given in Table 14.1. Refer to Amemiya (1985, p. 250) for details on the properties of nonlinear two-stage least squares.

Seemingly Unrelated Regression

If the regression equations are not simultaneous, so there are no dependent regressors, seemingly unrelated regression (SUR) can be used to estimate systems of equations with correlated random errors. The large-sample efficiency of an estimation can be improved if these cross-equation correlations are taken into account. SUR is also known as joint generalized least squares or Zellner regression. Formally, the ${\hat{{{\theta}}}}$ that minimizes

$\hat{S}_{n} = \frac{1}n \sum_{t=1}^n{q(y_{t}\hspace*{1pt}, x_{t}\hspace*{1pt},... ... \hat{{\Sigma}}^{-1} q(y_{t}\hspace*{1pt}, x_{t}\hspace*{1pt}, {{\theta}}})$

is the SUR estimator of the parameters.

The SUR method requires an estimate of the cross-equation covariance matrix, ${\Sigma}$ .PROC MODEL first performs an OLS estimation, computes an estimate, ${\hat{\Sigma}}$ , from the OLS residuals, and then performs the SUR estimation based on ${\hat{\Sigma}}$ .The OLS results are not printed unless you specify the OLS option in addition to the SUR option.

You can specify the ${\hat{\Sigma}}$ to use for SUR by storing the matrix in a SAS data set and naming that data set in the SDATA= option. You can also feed the ${\hat{\Sigma}}$ computed from the SUR residuals back into the SUR estimation process by specifying the ITSUR option. You can print the estimated covariance matrix ${\hat{\Sigma}}$ using the COVS option on the FIT statement.

The SUR method requires estimation of the ${\Sigma}$ matrix, and this increases the sampling variability of the estimator for small sample sizes. The efficiency gain SUR has over OLS is a large sample property, and you must have a reasonable amount of data to realize this gain. For a more detailed discussion of SUR, refer to Pindyck (1981, p. 331-333).

Three-Stage Least-Squares Estimation

If the equation system is simultaneous, you can combine the 2SLS and SUR methods to take into account both dependent regressors and cross-equation correlation of the errors. This is called three-stage least squares (3SLS).

Formally, the ${\hat{{{\theta}}}}$ that minimizes

$\hspace*{-0.40in}\hat{S}_{n} = \frac{1}n (\sum_{t=1}^n{(q(y_{t}\hspace*{1pt}, ... ...1}^n{(q(y_{t}\hspace*{1pt}, x_{t}\hspace*{1pt},{{\theta}}) {\otimes} z_{t})})$

is the 3SLS estimator of the parameters. For more details on 3SLS, refer to Gallant (1987, p. 435).

Residuals from the 2SLS method are used to estimate the ${\Sigma}$ matrix required for 3SLS. The results of the preliminary 2SLS step are not printed unless the 2SLS option is also specified.

To use the three-stage least-squares method, specify an INSTRUMENTS statement and use the 3SLS or N3SLS option on either the PROC MODEL statement or a FIT statement.

Generalized Method of Moments - GMM

For systems of equations with heteroscedastic errors, generalized method of moments (GMM) can be used to obtain efficient estimates of the parameters. See the "Heteroscedasticity" section for alternatives to GMM.

Consider the nonlinear model

${\epsilon}_{t}\hspace*{2pt} &=& q(y_{t}\hspace*{1pt}, x_{t}\hspace*{1pt}, {{\theta}}) \cr z_{t} &=& Z(x_{t})\hspace*{2pt}$

where z_t is a vector of instruments and ${\epsilon}$ _t is an unobservable disturbance vector that can be serially correlated and nonstationary.

In general, the following orthogonality condition is desired:

$E ({\epsilon}_{t} {\otimes} z_{t}) = 0$

which states that the expected crossproducts of the unobservable disturbances, ${{{\epsilon}}_{t}}$ , and functions of the observable variables are set to 0. The first moment of the crossproducts is

$m_{n} &=& \frac{1}n \sum_{t=1}^n{m(y_{t}\hspace*{1pt}, x_{t}\hspace*{1pt}, {{... ...}}) &=& q(y_{t}\hspace*{1pt}, x_{t}\hspace*{1pt}, {{\theta}}) {\otimes} z_{t}$

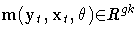where ${m(y_{t}\hspace*{1pt}, x_{t}\hspace*{1pt}, {{\theta}}){\in} R^{gk}}$ .

The case where gk > p is considered here, where p is the number of parameters.

Estimate the true parameter vector ${{\theta}^0}$ by the value of ${\hat{{\theta}}}$ that minimizes

$S({\theta}, V) = [n{m}_{n}({\theta})]' V\hspace*{1pt}^{-1}[n{m}_{n}({\theta})]$

where

$V = \rm{Cov}([n{m}_{n}({\theta}^0)], [n{m}_{n}({\theta}^0)]')$

The parameter vector that minimizes this objective function is the GMM estimator. GMM estimation is requested on the FIT statement with the GMM option.

The variance of the moment functions, V, can be expressed as

$V &=& E (\sum_{t=1}^n{{{\epsilon}}_{t} {\otimes} z_{t}}) (\sum_{s=1}^n{{{\eps... ...} {\otimes} z_{t}) ( {{\epsilon}}_{s} {\otimes} z_{s})']} \cr &=& n S_{n}^0$

where S_n⁰ is estimated as

$\hat{S}_{n} = \frac{1}n \sum_{t=1}^n \sum_{s=1}^n{(q(y_{t}\hspace*{1pt}, x_{t}... ...z_{t})(q(y_{s}\hspace*{1pt}, x_{s}\hspace*{1pt}, {{\theta}}) {\otimes} z_{s})'}$

Note that ${\hat{S}_{n}}$ is a gk×gk matrix. Because Var ${(\hat{S}_{n})}$ will not decrease with increasing n we consider estimators of S_n⁰ of the form:

$\hat{S}_{n}(l(n)) &=& \sum_{{\tau} = -n + 1}^{n-1}{w {{\tau} \overwithdelims ()... ...t-{\tau}}]'} & {\tau}\gt=0\space \cr (\hat{S}_{n,-{\tau}})' & {\tau}\lt\cr }$

where l(n) is a scalar function that computes the bandwidth parameter, w(·) is a scalar valued kernel, and the diagonal matrix D is used for a small sample degrees of freedom correction (Gallant 1987). The initial ${{\theta}^{\char93 }}$ used for the estimation of ${\hat{S}_{n}}$ is obtained from a 2SLS estimation of the system. The degrees of freedom correction is handled by the VARDEF= option as for the S matrix estimation.

The following kernels are supported by PROC MODEL. They are listed with their default bandwidth functions:

Bartlett: KERNEL=BART

$w(x) &=& \cases{ 1-| x| & | x|\lt= 1\space \cr 0 & otherwise \cr } \cr l(n) &=& \frac{1}2 n^{1 / 3}$

Parzen: KERNEL=PARZEN

$w(x) &=& \cases{ 1-6| x|^2+6| x|^3 & 0\lt=| x|\lt=\frac{1}2\space \cr 2(1-| ... ...rac{1}2\lt=| x|\lt=1\space \cr 0 & otherwise \cr } \cr l(n) &=& n^{1 / 5}$

Quadratic Spectral: KERNEL=QS

$w(x) &=& \frac{25}{12{\pi}^2 x^2} ( \frac{{sin}(6{\pi}x/5)}{6{\pi}x/5} - {cos}(6{\pi}x/5) ) \cr l(n) &=& \frac{1}2 n^{1 / 5}$

Figure 14.15: Kernels for Smoothing

Details of the properties of these and other kernels are given in Andrews (1991). Kernels are selected with the KERNEL= option; KERNEL=PARZEN is the default. The general form of the KERNEL= option is

      KERNEL=( PARZEN | QS | BART, c, e )

where the e >= 0 and c >= 0 are used to compute the bandwidth parameter as

l(n) = c n^e

The bias of the standard error estimates increases for large bandwidth parameters. A warning message is produced for bandwidth parameters greater than n^(1/3). For a discussion of the computation of the optimal l(n), refer to Andrews (1991).

The "Newey-West" kernel (Newey (1987)) corresponds to the Bartlett kernel with bandwith parameter l(n) = L +1. That is, if the "lag length" for the Newey-West kernel is L then the corresponding Model procedure syntax is KERNEL=( bart, L+1, 0).

Andrews (1992) has shown that using prewhitening in combination with GMM can improve confidence interval coverage and reduce over rejection of t-statistics at the cost of inflating the variance and MSE of the estimator. Prewhitening can be performed using the %AR macros.

For the special case that the errors are not serially correlated, that is

$E{\ssbeleven (e_{t} {\otimes} z_{t})(e_{s} {\otimes} z_{s})} = 0 \hspace*{3em} t {\ne} s$

the estimate for S_n⁰ reduces to

$\hat{S}_{n} = \frac{1}n \sum_{t=1}^n{[q(y_{t}\hspace*{1pt}, x_{t}\hspace*{1pt}... ..._{t}] [q(y_{t}\hspace*{1pt}, x_{t}\hspace*{1pt}, {{\theta}}) {\otimes} z_{t}]'}$

The option KERNEL=(kernel,0,) is used to select this type of estimation when using GMM.

Testing Over-Identifying Restrictions

Let r be the number of unique instruments times the number of equations. The value r represents the number of orthogonality conditions imposed by the GMM method. Under the assumptions of the GMM method, r-p linearly independent combinations of the orthogonality should be close to zero. The GMM estimates are computed by setting these combinations to zero. When r exceeds the number of parameters to be estimated, the OBJECTIVE*N, reported at the end of the estimation, is an asymptoticly valid statistic to test the null hypothesis that the over-identifying restrictions of the model are valid. The OBJECTIVE*N is distributed as a chi-square with r-p degrees of freedom (Hansen 1982, p. 1049).

Iterated Generalized Method of Moments - ITGMM

Iterated generalized method of moments is similar to the iterated versions of 2SLS, SUR, and 3SLS. The variance matrix for GMM estimation is re-estimatedg at each iteration with the parameters determined by the GMM estimation. The iteration terminates when the variance matrix for the equation errors change less than the CONVERGE= value. Iterated generalized method of moments is selected by the ITGMM option on the FIT statement. For some indication of the small sample properties of ITGMM, refer to Ferson (1993).

Full Information Maximum Likelihood Estimation - FIML

A different approach to the simultaneous equation bias problem is the full information maximum likelihood (FIML) estimation method (Amemiya 1977).

Compared to the instrumental variables methods (2SLS and 3SLS), the FIML method has these advantages and disadvantages:

FIML does not require instrumental variables.
FIML requires that the model include the full equation system, with as many equations as there are endogenous variables. With 2SLS or 3SLS you can estimate some of the equations without specifying the complete system.
FIML assumes that the equations errors have a multivariate normal distribution. If the errors are not normally distributed, the FIML method may produce poor results. 2SLS and 3SLS do not assume a specific distribution for the errors.
The FIML method is computationally expensive.

The full information maximum likelihood estimators of ${\theta}$ and ${{\sigma}}$ are the ${\hat{{\theta}}}$ and ${\hat{{\sigma}}}$ that minimize the negative log likelihood function:

$l_{n}({{\theta}}, {{\sigma}}) = &\frac{ng}2& {\ln}(2{\pi}) - \sum_{t=1}^n{{\ln... ...*{1pt}, {{\theta}}) q'(y_{t}\hspace*{1pt}, x_{t}\hspace*{1pt}, {{\theta}})} )$

The option FIML requests full information maximum likelihood estimation. If the errors are distributed normally, FIML produces efficient estimators of the parameters. If instrumental variables are not provided the starting values for the estimation are obtained from a SUR estimation. If instrumental variables are provided, then the starting values are obtained from a 3SLS estimation. The negative log likelihood value and the l₂ norm of the gradient of the negative log likelihood function are shown in the estimation summary.

FIML Details

To compute the minimum of ${l_{n}({{\theta}}, {{\sigma}})}$ ,this function is concentrated using the relation:

${\Sigma}({\theta}) = \frac{1}n \sum_{t=1}^n{q(y_{t}\hspace*{1pt}, x_{t}\hspace*{1pt}, {{\theta}}) q'(y_{t}\hspace*{1pt}, x_{t}\hspace*{1pt}, {{\theta}})}$

This results in the concentrated negative log likelihood function:

$l_{n}({{\theta}}) = \frac{ng}2 (1 + {\ln}(2{\pi})) - \sum_{t=1}^n{{\ln}\biggl... ..._{t}\hspace*{1pt}, {{\theta}}) \biggr|} + \frac{n}2 {\ln} |{\Sigma}({\theta}|)$

The gradient of the negative log likelihood function is :

$\frac{{\partial}}{{\partial} {\theta}_{i}} l_{n}({{\theta}}) = \sum_{t=1}^n{{\nabla}_{i}(t)}$

$\hspace*{-0.65em} {\nabla}_{i}(t) &=& -{\rm tr}( ( \frac{{\partial}q(y_{t}\hs... ..._{t}\hspace*{1pt}, x_{t}\hspace*{1pt}, {{\theta}})} {{\partial} {\theta}_{i}}$

where

$\frac{{\partial}{\Sigma}({\theta})}{{\partial} {\theta}_{i}} = \frac{2}n \sum_{... ...}\hspace*{1pt}, x_{t}\hspace*{1pt}, {{\theta}})'} {{\partial} {\theta}_{i}} }$

The estimator of the variance-covariance of ${\hat{{\theta}}}$ (COVB) for FIML can be selected with the COVBEST= option with the following arguments:

CROSS

selects the crossproducts estimator of the covariance matrix (default) (Gallant 1987, p. 473):

$C = ( \frac{1}n \sum_{t=1}^n {{\nabla}(t) {\nabla}'(t)} )^{-1}$

where ${{\nabla}(t) = [{\nabla}_{1}(t), {\nabla}_{2}(t), { ... },{\nabla}_{p}(t)]'}$

GLS

selects the generalized least-squares estimator of the covariance matrix. This is computed as (Dagenais 1978)

$C = [ \hat{Z} ' ( {\Sigma}({\theta})^{-1} {\otimes} I) \hat{Z}]^{-1}$

where ${\hat{Z} = ( \hat{Z}_{1}, \hat{Z}_{2}, { ... },\hat{Z}_{p} )}$ is ng ×p and each ${\hat{Z}_{i}}$ column vector is obtained from stacking the columns of

$U \frac{1}n \sum_{t=1}^n{( \frac{{\partial}q(y _{t}\hspace*{1pt}, x_{t}\hspace*... ...ce*{1pt},{{\theta}})'} {{\partial} y_{n}^{'}{\partial} {\theta}_{i}} } - Q_{i}$

U is an n ×g matrix of residuals and q_i is an n ×g matrix ${\frac{{\partial}Q}{{\partial} {\theta}_{i}} }$ .

FDA

selects the inverse of concentrated likelihood Hessian as an estimator of the covariance matrix. The Hessian is computed numerically, so for a large problem this is computationally expensive.

The HESSIAN= option controls which approximation to the Hessian is used in the minimization procedure. Alternate approximations are used to improve convergence and execution time. The choices are

CROSS: The crossproducts approximation is used.
GLS: The generalized least-squares approximation is used (default).
FDA: The Hessian is computed numerically by finite differences.

HESSIAN=GLS has better convergence properties in general, but COVBEST=CROSS produces the most pessimistic standard error bounds. When the HESSIAN= option is used, the default estimator of the variance-covariance of ${\hat{{\theta}}}$ is the inverse of the Hessian selected.

Properties of the Estimates

All of the methods are consistent. Small sample properties may not be good for nonlinear models. The tests and standard errors reported are based on the convergence of the distribution of the estimates to a normal distribution in large samples.

These nonlinear estimation methods reduce to the corresponding linear systems regression methods if the model is linear. If this is the case, PROC MODEL produces the same estimates as PROC SYSLIN.

Except for GMM, the estimation methods assume that the equation errors for each observation are identically and independently distributed with a 0 mean vector and positive definite covariance matrix ${\Sigma}$ consistently estimated by S. For FIML, the errors need to be normally distributed. There are no other assumptions concerning the distribution of the errors for the other estimation methods.

The consistency of the parameter estimates relies on the assumption that the S matrix is a consistent estimate of ${\Sigma}$ .These standard error estimates are asymptotically valid, but for nonlinear models they may not be reliable for small samples.

The S matrix used for the calculation of the covariance of the parameter estimates is the best estimate available for the estimation method selected. For S-iterated methods this is the most recent estimation of ${\Sigma}$ . For OLS and 2SLS, an estimate of the S matrix is computed from OLS or 2SLS residuals and used for the calculation of the covariance matrix. For a complete list of the S matrix used for the calculation of the covariance of the parameter estimates, see Table 14.1.

Missing Values

An observation is excluded from the estimation if any variable used for FIT tasks is missing, if the weight for the observation is not greater than 0 when weights are used, or if a DELETE statement is executed by the model program. Variables used for FIT tasks include the equation errors for each equation, the instruments, if any, and the derivatives of the equation errors with respect to the parameters estimated. Note that variables can become missing as a result of computational errors or calculations with missing values.

The number of usable observations can change when different parameter values are used; some parameter values can be invalid and cause execution errors for some observations. PROC MODEL keeps track of the number of usable and missing observations at each pass through the data, and if the number of missing observations counted during a pass exceeds the number that was obtained using the previous parameter vector, the pass is terminated and the new parameter vector is considered infeasible. PROC MODEL never takes a step that produces more missing observations than the current estimate does.

The values used to compute the Durbin-Watson, R², and other statistics of fit are from the observations used in calculating the objective function and do not include any observation for which any needed variable was missing (residuals, derivatives, and instruments).

Details on the Covariance of Equation Errors

There are several S matrices that can be involved in the various estimation methods and in forming the estimate of the covariance of parameter estimates. These S matrices are estimates of ${\Sigma}$ ,the true covariance of the equation errors. Apart from the choice of instrumental or noninstrumental methods, many of the methods provided by PROC MODEL differ in the way the various S matrices are formed and used.

All of the estimation methods result in a final estimate of ${\Sigma}$ ,which is included in the output if the COVS option is specified. The final S matrix of each method provides the initial S matrix for any subsequent estimation.

This estimate of the covariance of equation errors is defined as

S = D(R'R)D

where R = (r₁, ... ,r_g) is composed of the equation residuals computed from the current parameter estimates in an n ×g matrix and D is a diagonal matrix that depends on the VARDEF= option. For VARDEF=N, the diagonal elements of D are ${1/\sqrt{n}}$ ,where n is the number of nonmissing observations. For VARDEF=WGT, n is replaced with the sum of the weights. For VARDEF=WDF, n is replaced with the sum of the weights minus the model degrees of freedom. For the default VARDEF=DF, the ith diagonal element of D is ${1/\sqrt{n-df_{i}}}$ , where df_i is the degrees of freedom (number of parameters) for the ith equation. Binkley and Nelson (1984) show the importance of using a degrees-of-freedom correction in estimating ${\Sigma}$ . Their results indicate that the DF method produces more accurate confidence intervals for N3SLS parameter estimates in the linear case than the alternative approach they tested. VARDEF=N is always used for the computation of the FIML estimates.

For the fixed S methods, the OUTSUSED= option writes the S matrix used in the estimation to a data set. This S matrix is either the estimate of the covariance of equation errors matrix from the preceding estimation, or a prior ${\Sigma}$ estimate read in from a data set when the SDATA= option is specified. For the diagonal S methods, all of the off-diagonal elements of the S matrix are set to 0 for the estimation of the parameters and for the OUTSUSED= data set, but the output data set produced by the OUTS= option will contain the off-diagonal elements. For the OLS and N2SLS methods, there is no previous estimate of the covariance of equation errors matrix, and the option OUTSUSED= will save an identity matrix unless a prior ${\Sigma}$ estimate is supplied by the SDATA= option. For FIML the OUTSUSED= data set contains the S matrix computed with VARDEF=N. The OUTS= data set contains the S matrix computed with the selected VARDEF= option. If the COVS option is used, the method is not S-iterated, and S is not an identity, the OUTSUSED= matrix is included in the printed output.

For the methods that iterate the covariance of equation errors matrix, the S matrix is iteratively re-estimated from the residuals produced by the current parameter estimates. This S matrix estimate iteratively replaces the previous estimate until both the parameter estimates and the estimate of the covariance of equation errors matrix converge. The final OUTS= matrix and OUTSUSED= matrix are thus identical for the S-iterated methods.

Nested Iterations

By default, for S-iterated methods, the S matrix is held constant until the parameters converge once. Then the S matrix is re-estimated. One iteration of the parameter estimation algorithm is performed, and the S matrix is again re-estimated. This latter process is repeated until convergence of both the parameters and the S matrix. Since the objective of the minimization depends on the S matrix, this has the effect of chasing a moving target.

When the NESTIT option is specified, iterations are performed to convergence for the structural parameters with a fixed S matrix. The S matrix is then re-estimated, the parameter iterations are repeated to convergence, and so on until both the parameters and the S matrix converge. This has the effect of fixing the objective function for the inner parameter iterations. It is more reliable, but usually more expensive, to nest the iterations.

R²

For unrestricted linear models with an intercept successfully estimated by OLS, R² is always between 0 and 1. However, nonlinear models do not necessarily encompass the dependent mean as a special case and can produce negative R² statistics. Negative R²'s can also be produced even for linear models when an estimation method other than OLS is used and no intercept term is in the model.

R² is defined for normalized equations as

$R^2 = 1 - \frac{SSE}{SSA - \bar{y}^2 x n}$

where SSA is the sum of the squares of the actual y's and ${\bar{y}}$ are the actual means. R² cannot be computed for models in general form because of the need for an actual Y.

Chapter Contents
Previous
Next
Top