Chaos in Vocal Cord Vibration –
A Look at the Evidences and Promises it Provide
By
Gina Jiang
MAT335H1S
Dr. Randall Pyke
Preface
Chaos Theory is considered
to be one of the three greatest scientific discoveries in the twentieth
century. In the early 1960's using a simple system of equations to model
convection in the atmosphere, Edward Lorenz, an MIT meteorologist, ran headlong
into "sensitivity to initial conditions". In the process he sketched
the outlines of one of the first recognized chaotic
attractors, and so came the birth of Chaos Theory.
The classical view of the natural world inclines us to categorize physical phenomena into overly simplistic dichotomy, which are determinism and randomness. A deterministic system follows a pattern that is regular, predicable, and stable; whereas a random system shows no pattern, and is irregular, erratic and unstable. When irregular behaviors are to observe in a deterministic system, they are often regarded as noise.
A more modern view of the physical world
is the notion of deterministic chaos. This resulted in the discovery that
systems governed by simple mathematical laws can behave in a highly
unpredictable way. Hence, even thought the result of such systems is determined
by the internal properties and the initial condition, predictability over the
long range is almost impossible. Nonlinear dynamics are used to analyze systems
of this type.
Introduction
Chaos,
or nonlinear dynamics, is a very useful tool in describing and explaining
system known as deterministic chaos. Applications of such system can be found
in stock markets, cognitive analysis in psychology, meteorology, etc. It has
also wildly captured attention in the biological science fields. In recent
years particularly, studies have been focused on analyzing chaotic properties
in Electroencephalographic (EEG) Activity, ventilatory system, heart rhythms, and vocal cord vibration. These
systems all share a common characteristic: they cannot be categorized as
random, as they all seem to follow its own determined patterns, yet their
outcomes are often highly unpredictable. The objective to these researches is
to hope to discover physiological patterns that distinguish normal functions
from the abnormal. Glass and Mackey even came up with a term called “Dynamic
Diseases” in 1988 to describe disorders in which normal organization is
disrupted and replaced by abnormal dynamics.
Chaos appears to shine a promising light
on providing clues to solve physiological problems that remain mysterious to
us. There are, however, three important criteria that must be all met before
applying chaos dynamic to the system. First the system must be deterministic
and nonlinear. Deterministic implies that the system is internally governed by
simple mathematical laws; nonlinear means that the input and outcome of the
system does not follow proportionality in any ways. The second criterion is that
the system must show a sudden qualitative change in its outcome, in other words
it must demonstrate property of bifurcation. Lastly, the system’s
representation of the phase space must show fractal property, which is
self-similarity. The simplest example that fulfills all three criteria is the
logistic equation, Xn=r(Xn-1)(1-Xn-1). It can
be observed from the following diagram (figure 1) that the logistic equation is
nonlinear yet follows a determined route in composing the graph. Clear
bifurcation points can also be spotted.

Figure 1: Bifurcation Diagram of the
Logistic Function
By enlarging a portion of figure 1, self-similarity of the diagram appeared in figure 2. And to verify that the pattern shown in figure 2 is non-random, an attractor diagram is plotted and a perfect parabola consists of disconnected dusts appear in view (figure 3).

Figure 2: Enlargement of a portion of
Figure 1

Figure 3: Attractor for the Logistic
Equation
Hence,
as one attempts to use chaos to describe a system, the three criteria describe
above must be met
Chaos
in Vocal Cord Vibration
Understanding vocal cord vibration is particular important to those
whose career heavily depends on singing and other vocal performances. For
instance, British actress Julie Andrews, who successfully portrayed sister
Maria in the classic movie The Sound of Music, captured generations
after generations with her angelic voice in singing My Favorite Things
and other memorable melodies. She lost her ability to hit high notes after a
vocal cord surgery in 1997, and since then she has been an active speaker in
many voice research conferences. Other important aspects in vocal cord research
are to help restore voice back to cancer patients whose vocal cords lost their
ability to vibrate. Therefore, vocal cord research definitely has its
importance in contributing to human health as a whole.
Before showing evidence of chaos found
in vocal cord vibration, several significant points must first be discussed,
starting with the mechanism of voice production.
Voice Production

Figure 4:
Voice Production Diagram
A)Vocal
cords closed immediately prior to phonation (voice production).
B) Air pressure develops below vocal cords because of air from lungs during
exhalation.
C) Vocal cords separate briefly with the release of air. (1) Arrow points to
the upper edge of the vocal cord.
D) Vocal cords re-approximate. (2) Arrow points to the lower edge of vocal
cord.
E) Vocal cords together again.
Limitations
Even though vocal cords occupy only a
small amount of space between epiglottis and trachea, there are many
contributing factors that make up a normal cord vibration. The unsteadiness in muscle contractions in the laryngeal and
respiratory system, turbulence in the glottal air stream, vortex shedding and instability
in the jet emerging from the glottis, asymmetry in the mechanical or
geometrical properties of the two vocal folds, nonlinearity in the mechanical
properties of vocal fold tissues, coupling between the vocal folds and the
vocal tract, mucus riding on the surface of vocal fold tissue are just a few
examples. Already, complicated interactions between the vocal parts are shown.
It is important to understand each factor individually before combining them
together for a complete conclusion. However, the difficulty also lies upon the
fact that it is very hard to isolate one factor from others since they all need
to work concurrently to produce sound.
Nonlinearity
in Vocal Fold Mechanics
In figure 5, it is shown that the stretched vocal muscle and the released muscle fail to produce a linear curve. The graph also provides evidence that the muscle tissue exhibit less stress during release than during stretched. The area between the two curves represents energy lost per cycle. This suggests that stress “leaks out” during the cycle, and not all energy is given back. Hence the nonlinear property of the vocal fold mechanic is demonstrated.

Figure
5: Stress-Strain curve for three cycles of stretch and release performed on
thyroarytenoid muscles.
Attractors
in Phase Space
The crucial condition for the
applicability of nonlinear dynamics is the dominance of a relatively low number
of variables in the system, xi(t) (i=1,2,…,m).
Then time-series can be projected into a phase space, which is spanned by these
m coordinates. And under the assumption of fixed parameters (external
conditions are held constant), the m-dimensional vector x(t), termed
trajectory, settles down on an attractor after some transient behavior. The
following diagram is an example of comparing normal vocal cord vibration with
an abnormal one. As it is shown, the coordinates settled at a fixed pattern,
i.e. an attractor, after a series of behavior. Also notice the abnormal cord
vibration attractor diagram, even though it doesn’t exhibit an as clean diagram
as the normal vibration, a determined pattern is still obviously shown.

Figure
6: Example of Attractors of
Attractor
in Dimensions and Lyapunov Exponents
Dimension is a measure of irregularity.
Likewise, attractor in dimensions is a quantitative characterization of the
attractor. Scaling
behavior of various quantities can be exploited to define dimensions, and
chaotic attractors typically have a noninteger dimension
Lyapunov
Exponent λ is useful to describe the
stability properties of trajectories. A positive Lyapunov exponent is an
indication of the presence of chaos, since forλ>0 sufficiently small deviations from a trajectory grow,
and it demonstrates a strong instability within the attractor. The inherent
instability of chaotic systems implies limited predictability of the future if
the initial state is know with only finite precision.
Therefore, with the aid of attractor dimension and the Lyapunov exponent, chaos can be distinguished from noise.

Figure 7: Summary Table of Various Attractors and their Characteristics
Bifurcations
Bifurcation, in other words, period doubling, simply means a limit cycle loses its stability and a periodic orbit of the double period is born. The appearance of bifurcations is often precursors to a chaotic dynamics.
Evidences for the Chaotic Nature of Voice Production
Human
being often uses voice to characterize individuals. Other observable vocal
phenomena that are presumably manifestations of nonlinear dynamics are
roughness of voice, creaky voice, voice breaks. Three studies conducted in the
early 90s provided scientific explanation to the chaotic nature of voice
production; they are also the pioneer studies in the demonstration of
nonlinearity in human vocal cord vibration.
Mathematical Models for Phonatory Function
The first to mention is the mathematical models designed by Awrejcewicz in 1990. In his study, Bifurcation Protrait of the Human Vocal Cord Oscillations, he bypassed the difficulty of conducting physiologic experiments on the phonating larynx, and demonstrated laryngeal function through his mathematical model. There he had shown that an important class of laryngeal model is indeed chaotic, as it produced bifurcations of all the behaviors that have been considered in the case of predictive equation.
Normal Infant Cry
The
second important study was conducted by Herzel, Mende, and Wermke, also in the
early 90s. They observed and took recordings of newborn infant cry vibrations
on spectrogram.(figure 8).

Figure 8: Spectrogram from a newborn infant
cry
They recognized that newborn infant cries are a rich
source of vocal characteristics rare or unknown in the adult voice. They also
shown that among the most salient and puzzling are the phenomena labeled
“subharmonic breaks” and “turbulence” which involve period-doubling and
aperiodicity, respectively.
Abnormal Phonation of Adults with Laryngeal Disorder
The third study was performed by Baken
in 1990. He compared the vocal cord vibrations between normal human and
patients with demonstrable laryngeal disorder. As shown in figure 9, both
normal and pathological vocal cord vibrations show observable patterns, despite
the variation in degree of of turbulence and vibration.
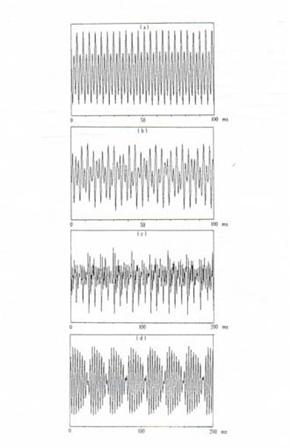
Figure 9: Acoustic waveform from sustained vowels. The top one was produced by a normal subject, whereas the latter three were produced by patients pathological vocal cord disorders
Baken further pointed out in his study that his data recording from both normal subjects and
disorder patients share qualitative similarity to the bifurcations seem in the
output of the mathematical models from Awrejcewicz’s study and in the voices of
infants from Herzel et al study. Baken’s study therefore provide dual
purposes: one is to show the deterministic chaos property in both normal and
abnormal vocal cord vibration; second is to reconfirm studies by Herzel and
awrejcewicz.
Conclusion
The
theory of nonlinear dynamics offers tools for evaluating and quantifying the
specific characteristics of the dynamical system that produces chaotic outputs.
In this report, specific example has been focused on vocal cord vibration. It
seems indisputable that the vocal system is chaotic. This means that a model is
created to include the unpredictable events and the bizarre products of vocal
disorder. This method also offers the potential of accurate differential
diagnosis based on acoustic and physiologic measurement
Future
Promises
Despite the promises chaotic dynamic offers to the vocal
cord research, there are still plenty of difficulties lying ahead. Data from a
real physical system are notoriously hard to deal with. They inevitably include
stochastic functions and cannot be made immune to the influences of
contaminating variables.
However, with the aid of advanced computer technology and
simulation, currently research laboratories around the world are still working
on discovering the value of nonlinear dynamic approaches to voice, and in
search of links between vocal disorder and brain neural activity. Hopefully in
the future voice pathology could be predicted and prevented at earlier stage in
life. Once chaos can be controlled, it will provide an alternative
treatment for a much more effective rehabilitation of the heretofore more
intractable categories of dysphonia
Reference
Calls out of chaos: the adaptive significance of nonlinear phenomena in mammalian vocal production: Fitch, Tecumse, Neubauer, Jrgen; Herzel,-Hanspeter. Animal Behaviour v 63 no3 Mar 2002. p. 407-18
What's in a voice: Titze,-Ingo: New Scientist v 147 Sept 23 1995. p. 38-42
Epilogue: Into a Chaotic Future: Baken RJ: In Rubin JS, Sataloff RT, Korovin GS, Gould WJ (eds): Diagnosis and Treatment of Voice Disorders, Igaku-Shoin, New York, 1995, pp. 502-509
Irregularity
of Vocal Period and Amplitude: A First Approach to the Fractal Analysis of
Voice: Baken RJ: Journal of Voice, 1990; 4:185-197
Bifurcation Portrait of the Human Vocal Cord Oscillations: Awrejcewicz J: Journal of Sound and Vibration, 1990; 136:151-156
Bifurcations and Chaos in Newborn Infant Cries: Mende W, Herzel H, Wermke K: Physics Letters A, 1990; 145:418-424
Evidence of Chaos in Vocal Fold Vibration: Titze IR, Baken RJ, Herzel H: In Titze IR (ed): Vocal Fold Physiology: Frontiers in Basic Science, San Diego, CA, Singular Publishing Group, 1993, p 143-188
Bifurcations and Chaos in Voice Signals: Herzel M: Applied Mechanics Review, 1993; 46:399-413
Bifurcations in an Asymmetric Vocal-fold Model: Steinecke I, Herzel M: The Journal of the Acoustical Society of America, 1995; 97(3):1874-1884
Nonlinearity, Complexity, and Control in Vocal Systems: Fletcher N: In Davis P, Fletcher N (eds): Vocal Fold Physiology: Controlling Chaos and Complexity. Singular Publishing Group, San Diego, CA 1996; 3-16
APOLONN Brings us to the Real World; Learning Nonlinear Dynamics and Fluctuations in Nature: Sato M, Joe K, Hirahara T: ATR Auditory and Visual Perception Research Laboratories, 1990; 1: I-581-I-586
Peitgen H, Jurgens H, Saupe D: Chaos and Fractals –
New Frontiers of Science. Springer, New York, NY 1992.