Deterministic Chaos in the Cardiac System

François Roy

MAT335

Dr. Randall Pyke

April 7^th, 2002

Contents

Preface …………………………………………………………………………… 3

Introduction ……………………………………………………………………… 3 Feedback Mechanisms …………………………………………………………… 4

Dynamic Systems and Chaos …………………………………………………….. 6

Unstable Periodic Orbits …………………………………………………………. 8

Time Scales ………………………………………………………………………. 10

Fractal Dimension ………………………………………………………………... 12

Chaos Control ……………………………………………………………………. 16

Conclusion ……………………………………………………………………….. 18

References ……………………………………………………………………….. 20

Preface

In recent years, cardiovascular diseases have posed major threats to human life. When studying cardiac diseases and their possible therapies, it is important to understand the pathological (diseased) changes that occur in the cardiac system. Healthy cardiac muscles contract periodically and are stimulated by electrochemical waves that spread throughout the heart. Thus, analysis of heart rates and electrocardiograms (ECGs) has proven to be a useful method for quantifying the efficiency of the heart. Recent studies have suggested that complex feedback mechanisms in the cardiovascular system are responsible for the underlying heart rate behaviour and heart rate variability (West et al., 1999). The cardiovascular system is governed by feedback mechanisms that regulate blood pressure, blood flow, blood ion concentrations, body temperature, and so on. Thus, the behaviour of the heart is generated from feedback systems and this strongly suggests that the heart behaves as a dynamic system.

Introduction

The hypothesis that the heart behaves as a dynamic system can be validated if instances of chaotic behaviour can be observed via the analysis of heart rates and electrocardiograms (ECGs). Fortunately, using the proper tools from dynamics and chaos, strong evidence of chaos has been observed. Thus, it is safe to assume that the variability in cardiac behaviour is generated via nonlinear dynamics. In this sense, the deterministic behaviour generated from the feedbacks can also yield a corresponding time series or data set similar to that of other dynamic systems including the logistic equation. When plotted properly, the points of the time series can generate graphs or pictures with a high degree of structure that would otherwise not occur from completely random series. Deterministic chaos further exhibits sensitive dependence on the initial conditions of the system. Thus, by using the Lyapunov exponent, a measure of divergence from initial conditions, further evidence of chaos has been observed in the cardiac system (Hagerman et al., 1996). Evidence of unstable periodic orbits (UPO) embedded in the cardiac rhythms has been discovered and can be used to describe the intrinsic properties of the attractors (Narayanan et al., 1997). The number of unstable periodic orbits found on the attractors of four different patients yields strong evidence that suggests that unstable periodic orbits can be used to quantify cardiac behaviour and diagnose the state of health of the cardiac system. It was also observed that time scales play an important role in the behaviour of the cardiac system (West et al., 1999). The appearance of highly periodic heart rates, similar to sine waves, and reduced time scales in cardiac diseased states support the notion that disease or cardiac failure is intrinsically linked to a loss in complexity. Self-similarity in the dynamic structure of heart rates, as seen on a heart rate vs time plots, reveals evidence of fractal dimension embedded in the behaviour of the cardiac system (Wagner et al., 1998). Recent algorithms attempting to calculate the fractal dimension of the heart rates have been developed to further improve the efficiency of measuring these abstract dimensions. These algorithms include the correlation dimension and the short-term fractal-scaling exponent. Recent application and development of chaotic models using nonlinear tools have allowed researchers to control the chaos of the cardiac system. Garfinkel et al. (1995) successfully controlled chaos in arrhythmic (irregular) heart rates by electronically perturbing heart rate contractions via a similar method outlined by Ott et al. (1990). This further suggests that the cardiac system behaves chaotically and can be controlled using the tools from nonlinear chaos. Thus, this paper explores the nonlinear dynamics of the cardiac system along with the nonlinear dynamical measures used to quantify and diagnose its behaviour.

Feedback Mechanisms

Rhythmic changes in heart rate have indicated that heart rate is not constant but varies significantly over time even in the absence of physical and mental stress. Analysis of heart rate oscillatory behaviour reveals a broad, noise-like variability over a large span of frequencies and suggests that the irregular variability and behaviour is due to nonlinearities in the control system of the cardiac network (Wagner et al., 1998). The specific mechanisms underlying heart rate behaviour and heart rate variability are certainly not very clear. However, strong evidence suggests that the heart rate is regulated by a complex feedback control mechanism involving closed control systems regulated via positive and negative feedbacks (West et al., 1999). The cardiovascular system is governed by feedback mechanisms that regulate blood pressure, blood flow, blood ion concentrations, body temperature, and so on. For example, if blood flow to the brain is significantly decreased, pressure receptors in the brain send signals to the heart demanding increased blood flow. The heart must respond to the brain’s demands by altering its current behaviour and increase its cardiac output. This example suggests that feedback or iteration processes form much of the backbone of cardiac behaviour in the body. As many feedbacks interact simultaneously on the cardiac system, it is clear that the heart needs complex integrating behaviour to respond to the body’s needs. Complexity in the feedback control indicates that the control system is in itself nonlinear. Current evidence suggests that the observed heart rate variability time series generated from nonlinear dynamics may be chaotic and deterministic in nature (West et al., 1999).

Dynamic Systems and Chaos

Garfinkel et al. (1995) attempted to discover the deterministic order and behaviour in the heart rate time series. Deterministic order implies that each point in a time series is generated by the previous point via subsequent iterations. An example of this is the standard logistic equation f(x) = ax(1-x) in which each point in the time series is generated via x_t+1 = f(x_t). 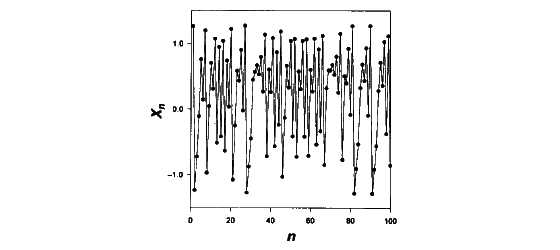Common irregularities in a time series of data points x₁, x₂, x₃,..., x_n are shown in figure 1 and can easily be thought to behave randomly. 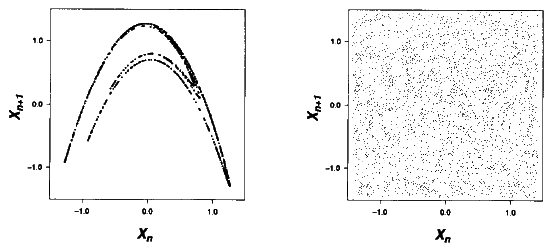In order to gather evidence of deterministic behaviour from an arbitrary time series, it is often useful to look at the data from a different perspective. By plotting the points of a time series on an x_n+1 vs x_n plot; pictures can often be generated with a high degree of structure called

Figure 1: Iteration of 100 points x₁, x₂, x₃, x₄ x₅,…, x₁₀₀ using the Hénon function (Garfinkel et al., 1995).

the attractor. The contrast between a deterministically generated times series and a random times series on a x_n+1 vs x_n plot can clearly be seen in Figure 2(a) and Figure 2(b) respectively. The high degree of structure in figure 2(a) composed of the elliptical cloud is certainly not what the random time series in Figure 2(b) could have generated. The presence of nonrandom structure in such a plot is generally a good diagnosis of deterministic chaos. Deterministic chaos further exhibits a number of characteristics that distinguish it from periodic or random behaviour. In particular, as seen for the logistic equation, dynamic systems have sensitive dependence on initial conditions. Thus, small changes in initial conditions have large pronounced effects on the behaviour of the system at some point in the future (Hagerman et al., 1996). This can often be manifested as divergence of adjacent trajectories that diverge widely as time or iteration evolves and can be measured via the Lyapunov exponent. Hagerman et al. (1996) discovered that by disrupting the behaviour of the cardiac system, the value of the largest Lyapunov exponent could be reduced. This further confirms the idea that the cardiac system

Figure 2(a): Iteration of 100 points x1, x2,…, x100 using the Hénon function (Garfinkel et al., 1995).

Figure 2(b): Iteration of 1000 points from random time series generates ergodic behaviour.

behaves chaotically and stresses the importance of using nonlinear dynamics as the tool for understanding the behaviour of the cardiac system.

Unstable Periodic Orbits

Further evidence suggests that chaos is inherent of the physiological control of heart rate via the discovery of unstable periodic orbits (UPO) in the cardiac rhythms. Narayanan et al. (1997) discovered that the periodicity and distribution of the orbits on the chaotic attractor are indicative of the state of health of the cardiac system. Unstable periodic orbits can be detected and extracted from chaotic attractors constructed from measured electrocardiograms and their importance arises from the properties of the attractors. In this sense, the intrinsic properties of the attractor can be expressed in terms of its unstable periodic orbits. Unstable periodic orbits can often be observed on the attractors of three-dimensional x_n+2 vs x_n+1 vs x_n plots and resemble loops. Attractors can themselves be created from heart rates and ECGs, but only using an appropriate delay time t (Narayanan et al., 1997). It is certainly more difficult to produce an attractor from ECGs since the time series cannot be obtained from a single equation such as the logistic equation. However, using a delay time t, it is possible to represent x₁, x₂, x₃,..., x_n with x(t), x(t + t), x(t + 2t),…, x(t + (n - 1)t) respectively and a corresponding attractor can subsequently be created. 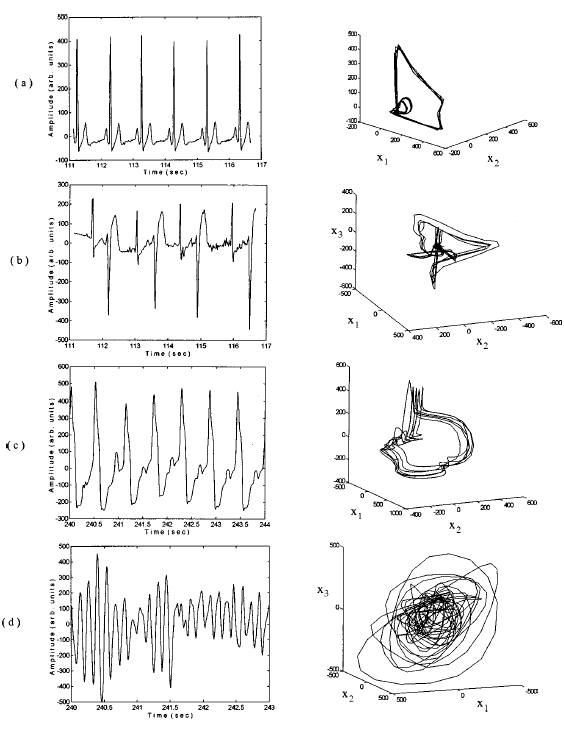This method has also been implemented in another one of this year’s MAT335 projects. Figures 3(a)-3(d) show ECG time series and three-dimensional views of the chaotic attractor for typically healthy and pathological diseased cases such as premature ventricular contraction (PVC), ventricular tachy arrhythmia (VTA), and ventricular fibrillation (VF) respectively. Importantly, the ECGs for the normal case can

Figure 3: ECG time series and attractors for (a) normal, (b) PVC, (c) VTA, and (d) VF cases respectively. x₁, x₂, and x₃ represent x(t), x(t + t), and x(t + 2t) respectively where x is the time series and t is the delay time (Narayanan et al., 1997).

be distinguished qualitatively from the others, but behaviour and structure of the chaotic attractors seem to yield differences that are more pronounced. Thus, by finding and extracting the unstable periodic orbits from the four attractors, Narayanan et al. (1997) discovered distinct quantitative differences for each of the cases. Figures 4(a) and 4(b) represent a comparison of the unstable periodic points for each of the five cases. The normal attractor of the cardiac systems is characterised by three or four unstable periodic orbits with typical periodicity and intensity where the strongest unstable periodic orbit is found to be in the range of m values 85-95 in arbitrary units and has a basic period of 0.94-1.05 seconds (Narayanan et al., 1997). In contrast to the healthy patients, the number of unstable periodic orbits varied significantly for the other four patients. This evidence further suggests that the cardiac system has been generated via nonlinear dynamics and often shows striking characteristics of chaos.

Figure 4 (a): Comparison of unstable periodic orbits of (a) healthy subject, (b) PVC, and (c) atrio ventricular block (Narayanan et al., 1997).

Figure 4 (b): Comparison of unstable periodic orbits of (a) healthy subject, (b) VTA, and (c) VF (Narayanan et al., 1997).

Time Scales

Intrinsically linked to the chaotic attractors of the cardiac system produced from ECGs, time scales play an important role in the behaviour of the cardiac system. The erratic behaviour of the ECG time series is a consequence of deterministic, nonlinear, and dynamic interactions between the biological components of the cardiac system (Ott et al., 1993). West et al. (1999) argue that the cardiac control system has innate properties that enable it to respond to a dynamic biological environment via scaling. The idea of scaling will become clearer later on. The chaotic motion or fluctuations in the time series include unstable periodic orbits that are used to move the system from one orbit to the next, thus giving the impression of randomness. Nevertheless, these apparent random fluctuations are what contain the information about the system. West et al. argue that this apparent random fractal time series in a biological context is the direct consequence of feedback control that operates over multiple time scales. In particular, heart rate interval fluctuations indicate that there exists long-term memory embedded in the randomness. This long-term memory is evident via the presence of an attractor as seen in Figure 2(a) as compared to randomness or the lack of memory in Figure 2(b). These long-term correlations or memories observed in the heart rate variability suggest that, although different regulatory mechanisms may act independently on different time scales, their dynamic effects on heart rate may be linked together via scaling. Thus, heart rate regulation would certainly be effected if one of the feedback mechanisms was impaired. Goldberger (1996) suggests that the cardiac system is self-organised in such a way that it has a characteristic time scale which gives it more plasticity and increases its ability to behave according to the feedbacks. 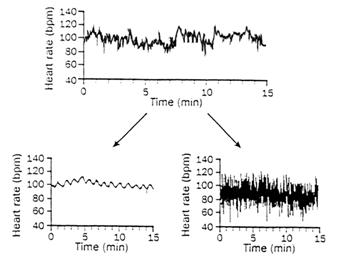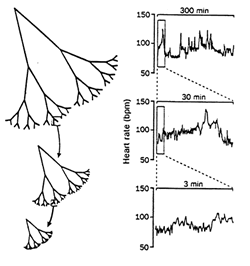The appearance of highly periodic dynamics or behaviours in many disease states is a compelling example which supports the notion that disease or cardiac failure is intrinsically linked to complexity loss and loss of time scales. Figure 5 represents examples of relative time scales of individuals in different cardiac

Figure 5: Healthy dynamics showing multiple scales (top), pathological breakdown to single scale sinus-rhythm (bottom left), and ventricular fibrillation randomness (Goldberger, 1996).

states. The normal and healthy dynamics show multiple time scales and fractal behaviour whereas the single scaled sinus-rhythm heart represents severe heart failure. The behaviour of atrial fibrillation is characterized by uncorrelated randomness and certainly would not pass any of the tests for deterministic chaotic as mentioned earlier. Thus, apparent fluctuations present in chaos contain information about the system and, by attempting to determine the information embedded in the time-series, it can prove to be beneficial to use the tools from chaos to analyse the cardiac system.

Fractal Dimension

Furthermore, evidence has indicated that scaling properties of heart rate behaviour can be quantified by the use of fractal dimension. Schematic representations of self-similar structure of dynamics in figure 6 suggest the importance of fractal dimension for understanding and analysing the heart rate fluctuations on different time scales. Importantly, all three of the graphs have a somewhat irregular appearance similar to that of coastlines or mountain ranges. Mechanically, Goldberger (1996) suggests that self-similarities in the heart rate serves a physiological function of rapid and efficient transport over a complex and spatially distributed system. Mathematically, fractal dimension is used to give a dimension of the statistical measure of the geometry of a cloud of points and can be assigned to any arbitrary data set (Wagner et al., 1998). Attractors produced from cardiac systems have revealed non-integer fractal dimensions (Mäkikallio et al., 2001). Standard algorithms for estimating fractal dimension require very large data sets (>10 000), thus newer algorithms have been developed to improve on data analysis. Conventional box counting methods can certainly be used to calculate the fractal dimension of curves generated from heart rates, however algorithms that are more efficient can operate with shorter sequences of points (Wagner et al., 1998). One of these algorithms calculating the correlation dimension is used to describe the complex structure of the cardiac attractor by approximating its fractal dimension (Hagerman et al., 1996). The correlation dimension algorithm proposed by Grassberger and Procaccia

Figure 6: Representation of self-similar structure and self-similar dynamics. The tree-like fractal has self-similarity such as fractal geometry in nature. The heart rate generates fluctuations of multiple time scales that are statistically self-similar (Goldberger, 1996).

(1983) attempts to extract information from the heart rate time series using another similar time delay t as outlined earlier (i.e. representing x₁, x₂, x₃,..., x_n with x(t), x(t + t), x(t + 2t),…, x(t + (n - 1)t)). By measuring the distance between every pair of points on the attractor, the correlation dimension can be calculated as:

where H(x) represents a heaviside step function. Via a bilogarithmic plot of C(N, r) vs r, the correlation dimension is an estimate of the slope of the plotted curve (Roa et al., 2001). The correlation dimension does not measure the fractal dimension of the heart rate per se, but harnesses the fractal-like structure or behaviour of the heart vs time curves. Varying estimates of the cardiac correlation dimension ranging from 3.6 to 5.2 by Babloyantz et al. (1988) to more recent values from 2.1 to 3.2 by Casseloggio et al. (1995) have been calculated. Recent algorithms exploring short-term fractal scaling analysis have been used to further quantify the fractal-like properties of heart rates (Mäkikallio et al., 2001). In this case, the root-mean square fluctuation of the time series is measured in each observation window and is plotted against the size of the window on a bilogarithmic scale. The mathematical reasoning behind the use of these algorithms is somewhat unclear, however, useful informative results have been obtained from these techniques. 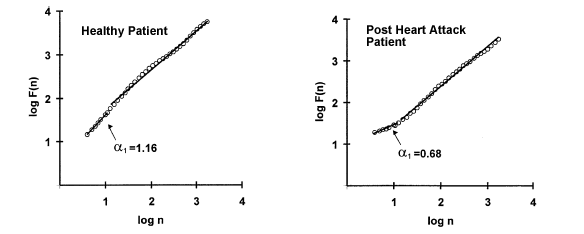The short-term fractal-scaling exponent a is calculated by approximating the slope of the curve and can be seen in figure 8. Using the short-term fractal-scaling exponent a₁ measured in the region where log(n) 1, Mäkikallio et al. (2001) suggest via the Kaplan-Meier survival curve (figure 9) that short-term fractal-scaling exponent a₁ is a good indicator of the state of health of the cardiac system. In the Kaplan-Meier survival curves, higher short-term fractal-scaling exponents a₁ had a significant survival advantage over the lower exponents a₁. This suggests that there is an intrinsic link between fractal-like dimension of heart rates and survival over time. Based on the data, I would certainly hope that my own personal short-term fractal scaling would be at least equal to 1. Thus, it is clear that fractal dimension, correlation dimension, and the short-term fractal exponent all play an important role in determining heart rate behaviour.

Figure 8: Typical example of short-term fractal-scaling exponent a₁ .The post heart attack patient has a short-term fractal-scaling exponent a₁ much smaller than a₁ of the healthy subject (Huikuri et al., 2001).

Figure 9: Kaplan-Meier survival curve of patients of various short-term scaling exponents a₁. Data in this figure correlates with figure 8 (Mäkikallio et al., 2001).

Chaos Control

Now having explored the cardiac system along with the tools used to model it, it is interesting to discover some of the useful applications that have been developed. Ott et al. (1990) showed that, by reducing the chaotic fluctuations within an acceptable range, it is even possible to control chaos. Ott et al. used the properties of the dynamics of stable and unstable manifolds of fixed points to control the chaos of the system. Near one of the unstable fixed points, a state point approaches the fixed point and then departs from it along preferred incoming and outgoing directions called the stable and unstable manifolds or saddle points. Ott et al. found a state point that wandered near a saddle point. Subsequent iterations allowed the state point to wander away from the saddle point along the unstable manifold. Thus, Ott et al. managed to use perturbations to move the stable manifold to the location of the state point so that the state point would essentially be sucked into the saddle point along the stable manifold in the following iterations. The state point subsequently approached the saddle point in the next iterations along the newly aligned stable manifold. In this way, Ott et al. managed to confine the state point

Figure 10: Ott et al. (1990) control scheme. (a) The nth iterate x_n falls near the unstable fixed point or saddle point x _f(P ₀). (b) Perturbation dp moves fixed point and corresponding stable and unstable manifolds. (c) The next iteration x _n+1 falls in the stable manifold. The state point is then attracted towards the saddle point along the newly aligned stable manifold (Garfinkel et al., 1995).

to a small neighbourhood of the saddle point thus subsequently controlling the chaos (figure 10). This technique outlined by Ott et al. has been extremely important for controlling the function of parts of the nervous system and is currently being used to further understand and model biological systems. Using similar techniques, Garfinkel et al. (1995) were able to convert irregular arrhythmic heart rates in 8 of 11 cases into normal periodic heart rates via the control of the heart’s chaos. The techniques used in these cases are no more complicated to understand than the ideas from simple dynamics including the logistic equation. In essence, the heart can be modelled as a simple pump. The behaviour of the pump oscillates between two phases; a filling phase and an emptying phase. Thus, for simplicity, the heart is modelled as a simple period-2 oscillator. 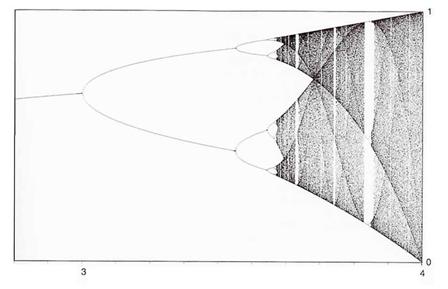Therefore, its behaviour can be modelled by means of the standard logistic equation f(x) = ax(1-x) in which the value of a lies in the interval 3.01 to 3.4 and the behaviour of the heart will be governed by the region in between the first and second

Figure 11: Final-state diagram for logistic equation and parameters a between 2.8 and 4 (Peitgen et al., 1992: 11.5)

bifurcation on the final state diagram (Figure 11). Therefore, the behaviour of the heart will oscillate between the filling phase and the emptying phase as predicted earlier. For a heart that beats completely irregularly, this model predicts that the behaviour of the heart can be characterised in the region of the final state diagram in which a 4. Thus, by controlling the value of a for the logistic equation and the simplified heart model, it is completely possible to control the behaviour of the heart. Often, electrical currents can be used to perturb the system and control the value of a and this technique is somewhat analogous to other techniques currently being used to control chaos. Thus, it is clear that the application of chaos control in biological systems will certainly prove to be useful for regulating the behaviour of the cardiac system.

Conclusion

This paper explores the nonlinear dynamics of the cardiac system along with the tools of chaos used to analyse and diagnose its behaviour. Studies suggest that complex feedback mechanisms in the cardiovascular system are responsible for the underlying heart rate behaviour and heart rate variability (West et al., 1999). The feedback mechanisms provide a complex control pattern that behaves deterministically via nonlinear dynamics. Thus, deterministic chaos of the cardiac system generated from the control systems yields a corresponding time series that shows a high degree of structure that would otherwise not be predicted from uncorrelated random points. Sensitive dependence on initial conditions along with behaviour of the Lyapunov exponent has been useful for characterizing the dynamic measure of the cardiac system (Hagerman et al., 1996). The presence of unstable periodic orbits embedded in the cardiac rhythms has also been used to quantify cardiac behaviour and diagnose the health state of the cardiac system (Narayanan et al., 1997). The appearance of highly periodic dynamics and reduced time scales in cardiac disease states supports the notion that disease or cardiac failure is intrinsically linked to a loss of complexity (West et al., 1999). Self-similarity in the dynamical structure of heart rates also reveals evidence of fractal dimension embedded in the behaviour of the cardiac system (Wagner et al., 1998). Evidence of the fractal dimension in the cardiac system can also be seen via correlation dimension and short-term fractal-scaling exponents implemented to improve the efficiency of dimensional analysis of the cardiac system. Nonetheless, evidence suggests that fractal dimension, correlation dimension, and the short-term fractal exponents are all intrinsically linked to the behaviour of the cardiac system. Recent applications and development of chaotic models using nonlinear tools from Garfinkel et al. (1995) and Ott et al. (1990) have indicated that the nonlinear systems can be controlled using the tools from chaos. Thus, it is clear that improving knowledge and understanding of mathematical chaos will inherently lead to an enhanced understanding of the complex behaviour of the cardiac system.

References

Anderson, J.L.; Karagounis L.A.; Stein K.M.; Moreno F.L.; Ledingham R.; Hallstrom A. 1997. Predictive value for future arrhythmic events of fractal dimension, a measure of time clustering of ventricular premature complexes, after myocardial infarction. Journal of the American College of Cardiology. 30(1): 226-232.

Babloyantz, A.; Destexhe, A. 1988. Biological Cybernetics. 58: 203.

Casaleggio, Aldo; Braiotta, Stefano. 1997. Estimation of Lyapunov Exponents of ECG Time Series: The Influence of Parameters. Chaos, Solitons & Fractals. 8(10): 1591-1599.

Casseloggio, A.; Corana, A. 1995. Chaos, Solitons & Fractals. 5: 713.

Garfinkel, A.; Weiss, J.N.; Ditto, W.L.; Spano, M.L. 1995. Chaos control of cardiac arrhythmias. Trends in Cardiovascular Medicine 5(2): 76-80.

Goldberger, Ary L. 1996. Non-linear dynamics for clinicians: chaos theory, fractals, and complexity at the bedside. The Lancet. 347: 1312-1314.

Grassberger, P.; Procaccia, I. 1983. Measuring the strangeness of the strange attractors. Physica D. 9: 189-208.

Hagerman, Inger; Berglund, Margareta; Lorin, Mikael; Nowak, Jacek; Sylvén, Christer. 1996. Chaos-related deterministic regulation of heart rate variability in time- and frequency domains: effects of autonomic blockade and exercise. Cardiovascular Research 31(3): 410-418.

Henon, M. 1976. A two-dimensional mapping with a strange attractor. Communications in Mathematical Physics. 50: 69-77.

Huikuri, Heikki V.; Mäkikallio, Timo H. 2001. Heart rate variability in ischemic heart disease. Autonomic Neuroscience. 90(1-2): 95-101.

Lampert, Rachel J. 1996. Diurnal Variation of Heart Rate Fractal Dimension in Heart Disease Patients. Journal of the American College of Cardiology. 27(2): 95A-96A.

Mäkikallio, Timo H.; Huikuri, Heikki V.; Hintze, Ulrik; Videbæk, Jorgen; Mitrani, Raul D.; et. al. 2001. Fractal analysis and time- and frequency-domain measures of heart rate variability as predictors of mortality in patients with heart failure. The American Journal of Cardiology. 87(2): 178-182.

Meesmann, M.; Boese, J.; et al. 1993. Demonstration of of 1/f fluctuations and white noise in the human heart rate by the variance-time-curve: implications for self-similarity. Fractals. 1: 312-320.

Narayana, K.; Govindan, R.B.; Gopinathan, M.S. 1997. Unstable periodc orbits in human cardiac rhythms. Physical Review E. 57(4): 4594-4603.

Ott, E.; Grebogi, C.; Yorke, J.A. 1990. Controlling chaos. Physical Review Letters. 64: 1196-1198.

Ott, E. 1993. Chaos in Dynamical Systems. Cambrigde University Press: New York.

Peitgen, H.O. :Jurgens, H.; Dietmar, S. 1992 Chaos and Fractals: New Frontiers of Science. Springer: New York.

Rao, R.K.A.; Yeragani, V.K. 2001. Decreased chaos and increased nonlinearity of heart rate time series in patients with panic disorder. Autonomic Neuroscience: Basic and Clinical. 88(1-2): 99-108.

Wagner, C.D.; Persson, P.B. 1998. Chaos in the cardiovascular system: An update. Cardiovascular Research 40(2): 257-264.

West, B.J.; Zhang, R.; Sanders, A.W.; Miniyar, S.; Zuckerman, J.H.; Levine, B.D. 1999. Fractal fluctuations in cardiac time series. Physica A 270(3-4): 552-566.