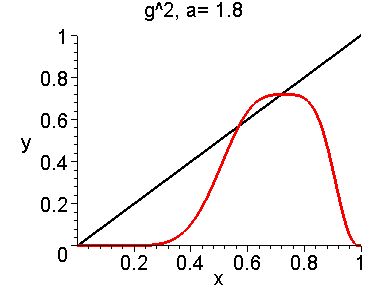
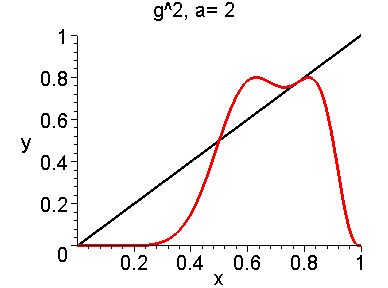
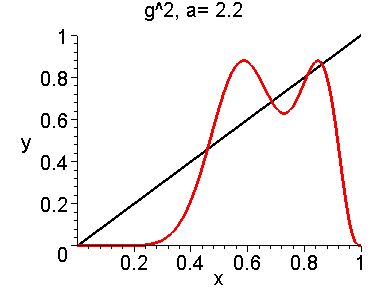
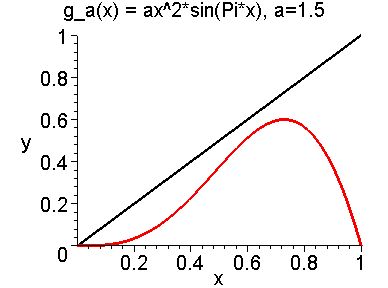
Period Doubling Bifurcation for ga(x) = ax2sin(Pi*x)
Here we have an example of a unimodal function, and by varying the parameter a we can see why it goes
through a period-doubling bifurcations just like the logistic family does. You can see for yourself the period-doubling
bifurcations of this function using the VB program Time Series.
The first two graphs are of ga for two different values of a;
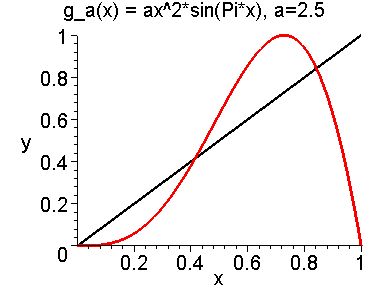
The next three graphs are of the second iterate g2 for different values of a. We
see that there is a period doubling bifurcation (period 1 to period 2) at a = 2 (2 period two
points bifurcated out from the the fixed point
on the right).