Applied Probabilistic Programming. Part I: RStan

class: center, middle, inverse, title-slide

# Applied Probabilistic Programming. Part I: RStan
## Practical Demonstration
### Renny Doig

---

# Overview

### 1. Example Dataset

### 2. Proposed Statistical Model

### 3. The Model as a Stan Program

### 4. Implementation in R

### 5. Analyzing Results

---
class: inverse, center, middle

# Example Problem Statement

---
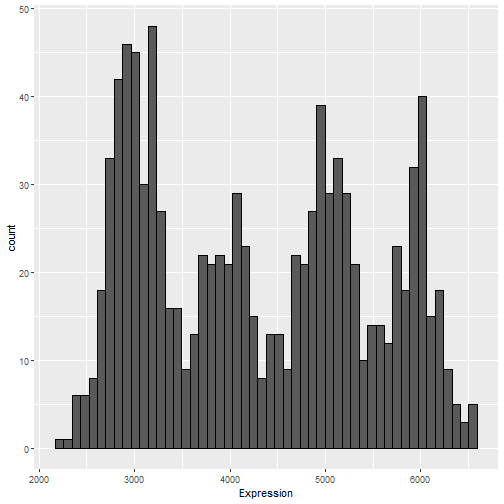
# Gene Expression Data

Suppose we have counts for the expression of the MT-ATP6 gene, taken from brain tissues from 1,000 subjects. We would like to make inference about the mean expression level for this gene which accounts for potential difference in means between types of brain tissue. In particular, we assume each sample is taken from one of the four following types:

.pull-left[
1. Cerebellum

1. Hippocampus

1. Hypothalamus

1. Brain stem

*Simulated data (modeled on GTEx)*

]

.pull-right[
<img src="tutorial_files/figure-html/unnamed-chunk-1-1.png" height="375px" />
]

---
class: inverse, center, middle

# Proposed Statistical Model

---
# Finite Gaussian Mixture Model

A *Gaussian mixture model* is a linear combination of Gaussian random variables, where each component corresponds to a sub-population and each weight is the probability of belonging to each sub-population

- In general, have `$K$` components (sub-populations)

- A randomly sampled individual belongs to component `$k\in\{1,\ldots,K\}$` with probability `$\alpha_k$`

- Random variable `$Z$` used to indicate sub-population: `$Z\sim\text{Categorical}(K,\pmb\alpha)$`

- An observation on an individual belonging to component `$k$` will be a `$Y|Z=k\sim\mathcal N(\mu_k,\sigma)$`

- Since `$Z$` is discrete it is incompatible with HMC

- The workaround is to marginalize out this indicator by evaluating the likelihood as a sum

`$$Y \sim \sum_{k=1}^K\alpha_k\mathcal N(\mu_k,\sigma)$$`

---
# Bayesian GMM

To make this model Bayesian, we need to assign prior distributions over the component proportions, means, and variance:

$$
`\begin{aligned}
Y|\pmb\alpha,\pmb\mu,\sigma &\sim \sum_{k=1}^K\alpha_k\mathcal N(\mu_k,\sigma) \\
\pmb\alpha &\sim \text{Dirichlet}(1) \\
\pmb\mu &\sim \text{Normal}(4000,1500) \\
\sigma^2 &\sim \text{InvGamma}(3,600^2)
\end{aligned}`
$$

- Dirichlet is a multivariate extension of the Beta distribution

- Used for a random vectors whose components take values in `$(0,1)$` and sum to 1
  
--

The resulting posterior distribution is:
`$$\pi(\pmb\alpha,\pmb\mu,\sigma|\mathbf y)\propto\prod_{i=1}^n\left[\sum_{k=1}^K\alpha_k\mathcal N(y_i|\mu_k,\sigma)\right]\mathcal N(\pmb\mu;4000,1500)\mathcal{IG}(\sigma^2;3,600^2)\mathcal D(\pmb\alpha;1)$$`

---
class: inverse, center, middle

# The Model as a Stan Program

---
# Basic Components of a Stan Program

Our model is specified in a separate .stan file

- Written in the Stan probabilistic programming language

- Contains up to seven blocks, each serving a different purpose

- We only need the three basic blocks:

1. `data{...}`: Specify all user input
  
  1. `parameters{...}`: Specify any parameters of the model which need to be estimated
  
  1. `model{...}`: Evaluates the log-posterior
  
- Stan uses this file to automatically construct a Hamiltonian Monte Carlo sampler for this model

---
# Variable Definition

The syntax for defining a variable in Stan is:

.center[`type<lower=a><upper=b>[dimension] name;`]

- `type`: Specifies type of variable

- Basic types are `int` and `real`
  
  - Can also have `vector`, `matrix`, and others

- `<lower=a>`: Specifies the lower bound of the variable; default is unbounded below

- `<upper=b>`: Specifies the upper bound of the variable; default is unbounded above

- `dimension`: Specifies dimension of the variable

- For `vector` it is the length
  
  - For `$n\times m$` `matrix` is specified `[n,m]`
  
---
# GMM: Data and Parameters

Now we can specify the `data` and `parameters` section of our RStan code:

```r
data {
 int<lower=1> n; // number of observations
 int<lower=2> K; // number of components
 vector[n] y; // observations
}

parameters {
 simplex[K] alpha; // mixing proportions
 ordered[K] mu; // means of components
 real<lower=0> sigma; // standard deviations of components
}
```

Identifiability: Without ordering `$\pmb\mu$`, the model is unidentifiable

- E.g. between two iterations, swap `$\mu_1$` and `$\mu_2$`

- This would leave the likelihood unchanged, and therefore the model is unidentifiable
  
- Imposing an ordering prevents this swapping

---
# Evaluating the Posterior

The log-posterior can be specified in two ways

- Suppose we want to model `$Y\sim\mathcal N(\mu,\sigma)$`

1. Distributional statement: `y ~ normal(mu, sigma);`

1. Increment statement: `target += normal_lpdf(y | mu, sigma);`

- `target` is a protected keyword and requires special functions to access

- These are equivalent statements; can have combination in your `model` block

- Both are vectorized, so if `y` is a vector, then it sums over all log-pdf evaluations

---
# Note on Log-Sum-Exponential

Recall in our posterior, we needed to evaluate `$\sum_{k=1}^K\alpha_k\mathcal N(y|\mu_k,\sigma)$`

- Since Stan operates on the log-posterior, we need the log of this quantity

- In terms of log-densities, this would be written as:
`$$\log\left(\sum_{k=1}^K\exp\left[\log(\alpha_k)+\log(\mathcal N(y|\mu_k,\sigma))\right]\right)$$`
- In Stan, if we have a vector `x=[a,b,c]`, the function `log_sum_exp(x)` will evaluate `$\log(\exp(a)+\exp(b)+\exp(c))$`

- This will be used to evaluate the log-posterior

---
# GMM: Model

Recall that the posterior we want to encode is:
`$$\pi(\pmb\alpha,\pmb\mu,\sigma|\mathbf y)\propto\prod_{i=1}^n\left[\sum_{k=1}^K\alpha_k\mathcal N(y_i|\mu_k,\sigma)\right]\mathcal N(\pmb\mu;4000,1500)\mathcal{IG}(\sigma^2;3,600^2)\mathcal D(\pmb\alpha;1)$$`

```r
model {
  // priors
  target += gamma_lpdf(1/sigma^2 | 3, 600^2);
  target += normal_lpdf(mu | 4000, 1500);
  target += dirichlet_lpdf(alpha | rep_vector(1, K));

// likelihood
  for(i in 1:n){
    vector[K] temp = log(alpha);
    
    for(k in 1:K){
      temp[k] += normal_lpdf(y[i] | mu[k], sigma);
    }
    
    target += log_sum_exp(temp);
  }
}
```

---
class: inverse, center, middle

# Implementation in R

---
# The RStan Package

The Stan software is accessed in R through the `rstan` package

General flow of implementation is

1. Create .stan file specifying our model

1. Read data into R and reformat to match the Stan program

1. Execute the `stan` function

- Automatically generate a Hamiltonian Monte Carlo sampler
  
  - Produce posterior samples, plus diagnostics

1. Generate plots, numerical summaries, etc.

Note on Compute Canada installation: may require manual installation of `V8`, `Rcpp`, or `RcppEigen` packages

---
# The `stan` function

The required arguments to the `stan` function are:

- `file`: A string indicating the path of the .stan file containing the model code

- `data`: A named list with elements matching those specified in the data block of the Stan file

Some optional, but often used arguments:

- `chains`: The number of MCMC chains used (default 4)

- `iter`: Total length of each chain (default 2000)

- `init`: A list or function used to initialize each chain (default "random")

- `seed`: The seed used for random number generation

A full list of parameters can be found in the CRAN documentation

---
# Sampling from the Bayesian GMM

```r
# load the RStan library
library(rstan)

# read in data
Expression <- read_csv("../Data/Expression.csv")$Expression

# enable parallel computing
options(mc.cores=5)

# set up data
n <- length(Expression)
K <- 4

stan_data <- list(n=n, K=K, y=Expression)
```

---
# Sampling from the Bayesian GMM

```r
# for the rdirichlet function
library(extraDistr)

# initial values
init_func <- function(){
 list(alpha = as.numeric(rdirichlet(1, rep(1, K))),
 mu = sort(rnorm(K, 4000, 1500)),
 sigma = 1 / sqrt(rgamma(1, 3, 600^2)))
}

# run stan
fit <- stan(file = "gaussian_mixture.stan",
 data = stan_data,
 chains = 5,
 iter = 1e4,
 init = init_func,
 seed = 2)
```

Note: If `seed` not supplied then Stan will set it randomly, overriding previously set seeds

---
class: inverse, center, middle

# Analyzing the Results

---
# Examples of Plots

.pull-left[

```r
library(bayesplot)

mcmc_areas(fit, regex_pars="alpha", prob=0.95) + theme(axis.text = element_text(size=20))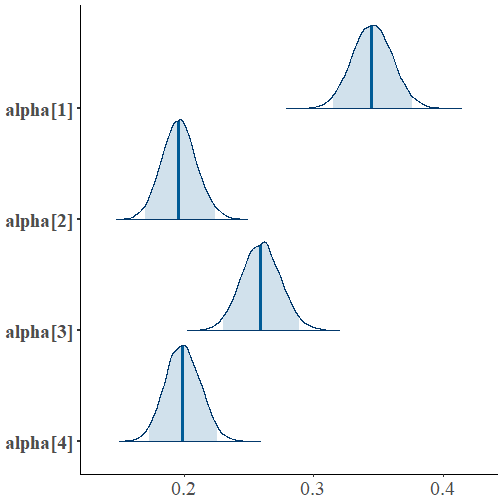
```

<img src="tutorial_files/figure-html/unnamed-chunk-7-1.png" height="350px" />
]

.pull-right[

```r
mcmc_areas(fit, regex_pars="mu", prob=0.95) + theme(axis.text = element_text(size=20))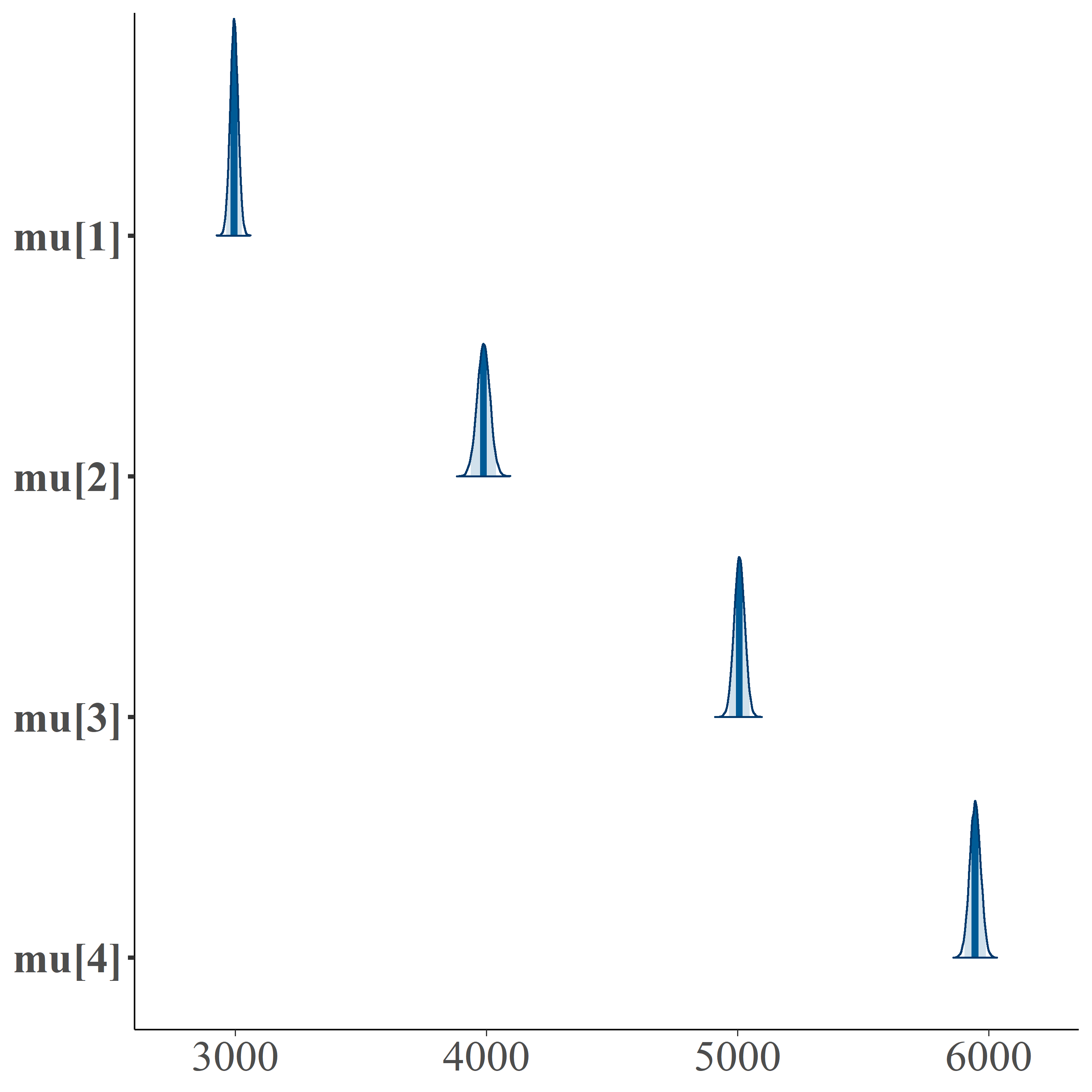
```

<img src="tutorial_files/figure-html/unnamed-chunk-8-1.png" height="350px" />
]

---
# Numerical Summary of Results

RStan also has a summary function for `stan-fit` objects:

```r
summ <- summary(fit)$summary
colnames(summ)
```

```
 [1] "mean"    "se_mean" "sd"      "2.5%"    "25%"     "50%"     "75%"    
 [8] "97.5%"   "n_eff"   "Rhat"   
```

```r
round(summ[rownames(summ)!="lp__", c("2.5%", "mean", "97.5%")],2)
```

```
            2.5%    mean   97.5%
alpha[1]    0.32    0.35    0.38
alpha[2]    0.17    0.20    0.22
alpha[3]    0.23    0.26    0.29
alpha[4]    0.17    0.20    0.23
mu[1]    2963.46 2994.70 3025.78
mu[2]    3936.70 3987.60 4038.10
mu[3]    4964.72 5006.32 5047.77
mu[4]    5902.28 5945.14 5987.92
sigma     249.41  263.07  278.16
```

---
# Extracting the Data

It might be preferable to just extract the samples from the `stanfit` object using the `extract` function

```r
par_fit <- extract(fit, pars="lp__", include=F)
```

- This returns a list of named matrices or vectors of posterior samples

- E.g. `par_fit$alpha` is a matrix with 4 columns, one for each `$\alpha_k$`
  
- `lp__` is the value of the log-posterior at each iteration
  
- `include` can be used to invert the meaning of `pars` (i.e. `lp__` is excluded from the extraction)

This can then be converted to a data frame

```r
par_fit <- as.data.frame(par_fit)
```

---
# Concluding Remarks

RStan provides a appealing Bayesian analysis software

- Probabilistic programming allows for flexibility; any model that can be written in the Stan languange can be sampled from

- A Hamiltonian Monte Carlo sampler is automatically created and executed to sample from the posterior

- The package is well-maintained; no debugging of the algorithm itself necessary

These slides can be found here: https://www.sfu.ca/~rennyd/RStanTutorial/tutorial.html

- Supporting files can be found in the parent directory