STAT 804: Lecture 16 Notes
Distribution theory for sample autocovariances
The simplest statistic to consider is
![]()
where the sum extends over those t for which the data are available. If the series has mean 0 then the expected value of this statistic is simply
![]()
which differs negligibly for T large compared to k from ![]() .
To compute the variance we begin with the second moment which is
.
To compute the variance we begin with the second moment which is
![]()
The expectations in question involve the fourth order product
moments of X and depend on the distribution of the X's and
not just on ![]() . However, for the interesting case of white
noise, we can compute the expected value. For k > 0 you may assume
that s < t or s=t since the s > t cases can be figured out by swapping
s and t in the s < t case. For s < t the variable
. However, for the interesting case of white
noise, we can compute the expected value. For k > 0 you may assume
that s < t or s=t since the s > t cases can be figured out by swapping
s and t in the s < t case. For s < t the variable ![]() is independent
of all 3 of
is independent
of all 3 of ![]() ,
, ![]() and
and ![]() . Thus the expectation factors
into something containing the factor
. Thus the expectation factors
into something containing the factor ![]() . For s=t,
we get
. For s=t,
we get ![]() . and so the second
moment is
. and so the second
moment is
![]()
This is also the variance since, for k > 0 and for white noise,
![]() .
.
For k=0 and s < t or s > t the expectation is simply
![]() while for s=t we get
while for s=t we get ![]() .
Thus the variance of the sample variance (when the mean is known
to be 0) is
.
Thus the variance of the sample variance (when the mean is known
to be 0) is
![]()
For the normal distribution the fourth moment ![]() is given simply
by
is given simply
by ![]() .
.
Having computed the variance it is usual to look at the large
sample distribution theory. For k=0 the usual central limit theorem
applies to ![]() (in the case of white noise) to prove that
(in the case of white noise) to prove that
![]()
The presence of ![]() in the formula shows that the approximation is
quite sensitive to the assumption of normality.
in the formula shows that the approximation is
quite sensitive to the assumption of normality.
For k > 0 the theorem needed is called the m-dependent central limit theorem; it shows that
![]()
In each of these cases the assertion is simply that the statistic in question divided by its standard deviation has an approximate normal distribution.
The sample autocorrelation at lag k is
![]()
For k > 0 we can apply Slutsky's theorem to conclude that
![]()
This justifies drawing lines at ![]() to carry
out a 95% test of the hypothesis that the X series is white
noise based on the kth sample autocorrelation.
to carry
out a 95% test of the hypothesis that the X series is white
noise based on the kth sample autocorrelation.
It is possible to verify that subtraction of ![]() from the
observations before computing the sample covariances does not
change the large sample approximations, although it does affect
the exact formulas for moments.
from the
observations before computing the sample covariances does not
change the large sample approximations, although it does affect
the exact formulas for moments.
When the X series is actually not white noise the situation is more complicated. Consider as an example the model
![]()
with ![]() being white noise. Taking
being white noise. Taking
![]()
we find that
![]()
The expectation is 0 unless either all 4 indices on the
![]() 's are the same or the indices come in two pairs of equal
values. The first case requires
's are the same or the indices come in two pairs of equal
values. The first case requires ![]() and
and ![]() and then
and then
![]() . The second case requires one of three pairs of equalities:
. The second case requires one of three pairs of equalities:
![]() and
and ![]() or
or
![]() and
and ![]() or
or
![]() and
and ![]() along with the restriction
that the four indices not all be equal. The actual moment is then
along with the restriction
that the four indices not all be equal. The actual moment is then
![]() when all four indices are equal and
when all four indices are equal and ![]() when there
are two pairs. It is now possible to do the sum using geometric
series identities and compute the variance of
when there
are two pairs. It is now possible to do the sum using geometric
series identities and compute the variance of ![]() .
It is not particularly enlightening to finish the calculation in
detail.
.
It is not particularly enlightening to finish the calculation in
detail.
There are versions of the central limit theorem called mixing central limit theorems which can be used for ARMA(p,q) processes in order to conclude that
![]()
has asymptotically a standard normal distribution and that the same is true when the standard deviation in the denominator is replaced by an estimate. To get from this to distribution theory for the sample autocorrelation is easiest when the true autocorrelation is 0.
The general tactic is the ![]() method or Taylor expansion. In this
case for each sample size T you have two estimates, say
method or Taylor expansion. In this
case for each sample size T you have two estimates, say ![]() and
and ![]() of two parameters. You want distribution theory for the ratio
of two parameters. You want distribution theory for the ratio
![]() . The idea is to write
. The idea is to write ![]() where
f(x,y)=x/y and then make use of the fact that
where
f(x,y)=x/y and then make use of the fact that ![]() and
and ![]() are
close to the parameters they are estimates of. In our case
are
close to the parameters they are estimates of. In our case ![]() is the sample autocovariance at lag k which is close to the
true autocovariance
is the sample autocovariance at lag k which is close to the
true autocovariance ![]() while the denominator
while the denominator ![]() is the
sample autocovariance at lag 0, a consistent estimator of
is the
sample autocovariance at lag 0, a consistent estimator of ![]() .
.
Write
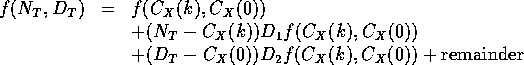
If we can use a central limit theorem to conclude that
![]()
has an approximately bivariate normal distribution and if we can neglect the remainder term then
![]()
has approximately a normal distribution. The notation here is that
![]() denotes differentiation with respect to the jth argument
of f. For f(x,y) = x/y we have
denotes differentiation with respect to the jth argument
of f. For f(x,y) = x/y we have ![]() and
and ![]() .
When
.
When ![]() the term involving
the term involving ![]() vanishes and we
simply get the assertion that
vanishes and we
simply get the assertion that
![]()
has the same asymptotic normal distribution as
![]() .
.
Similar ideas can be used for the estimated sample partial ACF.
center Portmanteau tests
In order to test the hypothesis that a series is white noise using the
distribution theory just given, you have to produce a single statistic
to base youre test on. Rather than pick a single value of k the
suggestion has been made to consider a sum of squares or a weighted
sum of squares of the ![]() .
.
A typical statistic is
![]()
which, for white noise, has approximately a ![]() distribution.
(This fact relies on an extension of the previous computations to conclude
that
distribution.
(This fact relies on an extension of the previous computations to conclude
that
![]()
has approximately a standard multivariate distribution. This, in turn, relies
on computation of the covariance between ![]() and
and ![]() .)
.)
When the parameters in an ARMA(p,q) have been estimated by maximum likelihood the degrees of freedom must be adjusted to K-p-q. The resulting test is the Box-Pierce test; a refined version which takes better account of finite sample properties is the Box-Pierce-Ljung test. S-Plus plots the P-values from these tests for 1 through 10 degrees of freedom as part of the output of arima.diag.