


Postscript version of these notes
STAT 804
Lecture 23 Notes
Estimating the spectrum
We now consider the quality of
 as an estimate of
as an estimate of  . We
have already shown that
. We
have already shown that
However we will see that the variance of this estimate  of
of  does
not go to 0 so that the estimate is not consistent.
does
not go to 0 so that the estimate is not consistent.
It is easier technically to consider the case of a normal mean 0
process  . For
normal data the real and imaginary parts of
. For
normal data the real and imaginary parts of  have normal distributions.
Both have mean 0. The variances are
have normal distributions.
Both have mean 0. The variances are
and
while the covariance between the real and imaginary parts is
Consider as an example the covariance, and use the usual complex
exponential identities to write the covariance as
Now make the change of variables  and
and  in the double sum.
The variable
in the double sum.
The variable  runs from
runs from  to
to  while when
while when  is fixed the
possible values of
is fixed the
possible values of  run, for
run, for  positive from
positive from  to
to  by
increments of 2 and, for
by
increments of 2 and, for  negative from
negative from  to
to  by increments
of 2. For each value of
by increments
of 2. For each value of  there are then
there are then  possible values of
possible values of  and the covariance becomes
The last two terms, involving
and the covariance becomes
The last two terms, involving  only, are
The terms
only, are
The terms  and
and  cancel each other while the term with
cancel each other while the term with  is 0
itself so that this term is 0.
is 0
itself so that this term is 0.
The terms above involving  may be simplified by using geometric series
to do the inside sums over
may be simplified by using geometric series
to do the inside sums over  . The result is a coefficient of
. The result is a coefficient of  which is bounded (bounded by
which is bounded (bounded by
 for instance. Then
since
for instance. Then
since
we have checked that the covariance between the real and imaginary parts of
 converges to 0 as
converges to 0 as
 .
.
Our previous calculations of the expectation of
 can be mimicked to show that the two variances each converge to
can be mimicked to show that the two variances each converge to
 . It follows that the vector
. It follows that the vector
 converges to a bivariate standard normal.
The squared length of this vector then converges in distribution to
the squared length of a standard bivariate normal which is exactly
converges to a bivariate standard normal.
The squared length of this vector then converges in distribution to
the squared length of a standard bivariate normal which is exactly
 or exponential with mean 2.
or exponential with mean 2.
Summary:
 converges in distribution to an
exponential random variable with mean
converges in distribution to an
exponential random variable with mean  . In particular,
. In particular,
 is not a consistent estimator of
is not a consistent estimator of  .
.
Improved estimates
To get better estimates we need either to resort to parametric estimation
techniques or do some smoothing. We will look at the latter idea first.
If  is smooth in the neighbourhood of some
is smooth in the neighbourhood of some  then we
can take estimates of
then we
can take estimates of  at a number of points nearby to
at a number of points nearby to
 and average them somehow. Averaging will reduce the variance
though it will introduce bias usually because the things being averaged all
have different expected values.
and average them somehow. Averaging will reduce the variance
though it will introduce bias usually because the things being averaged all
have different expected values.
The simplest kind of estimator is a moving average - we define
It turns out that the quantities being averaged are asymptotically
independent so that the estimate has the same distribution as an average
of  exponentials which is just a chi-squared with
exponentials which is just a chi-squared with  degrees
of freedom multiplied by
degrees
of freedom multiplied by
 . It is possible then to
produce a consistent estimate by letting
. It is possible then to
produce a consistent estimate by letting  grow slowly with
grow slowly with  but we
won't investigate this rather mathematical problem carefully here.
but we
won't investigate this rather mathematical problem carefully here.
Other weighted averages are possible; several are implemented in the
S-Plus function spectrum. Here are some points to note about
this estimation problem:
- Each estimate
 has expected value
has expected value
 where a (complicated) formula for the
bias can be deduced from the algebra above. The expected value of
an estimate of the form
is then
If
where a (complicated) formula for the
bias can be deduced from the algebra above. The expected value of
an estimate of the form
is then
If  is roughly linear around
is roughly linear around  then the first term will
be quite close to
then the first term will
be quite close to  when the weights make the estimate an
average, that is, they sum to 1. However, this approximation will be poor
in the neighbourhood of any peak in the spectrum which will be flattened
by this averaging. The second term in the expectation, on the other hand,
has no particular reason to average out to 0; increasing
when the weights make the estimate an
average, that is, they sum to 1. However, this approximation will be poor
in the neighbourhood of any peak in the spectrum which will be flattened
by this averaging. The second term in the expectation, on the other hand,
has no particular reason to average out to 0; increasing  without
dealing with this bias will eventually be fruitless as the bias becomes
the dominant component in the error. A common tactic to dealing with this
bias is tapering, where we compute
and use as a periodogram
where the tapering function
without
dealing with this bias will eventually be fruitless as the bias becomes
the dominant component in the error. A common tactic to dealing with this
bias is tapering, where we compute
and use as a periodogram
where the tapering function  typically decreases to 0 at 0 and at 1.
typically decreases to 0 at 0 and at 1.
- The ideal time to smooth the periodogram is when the spectrum
is flat, that is, when the series is white noise. If
 is a
filter such that
is a
filter such that
 is nearly white noise then we could
is nearly white noise then we could
- Transform
 to
to  .
.
- Compute the periodogram of
 .
.
- Smooth this periodogram fairly heavily, because there should
be no significant peaks in
 . Call the resulting estimate
. Call the resulting estimate
 .
.
- Estimate
 by
where
by
where  is the frequency response function of the filter
is the frequency response function of the filter  .
.
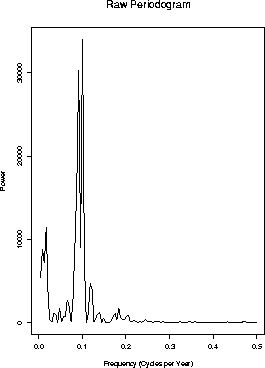
Here are several spectral estimates for the spectrum of the
sunspots series:
- The raw periodogram. Are there two peaks near a period of 10 years?
Is there a peak near 40 years?
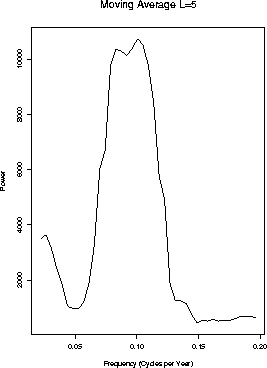
- Running means with
 .
.

- Running means
 .
.
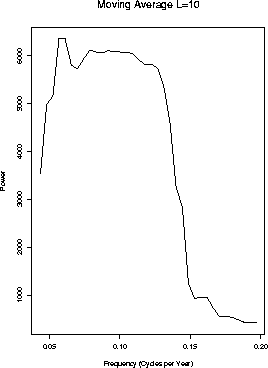
- Running means
 .
.
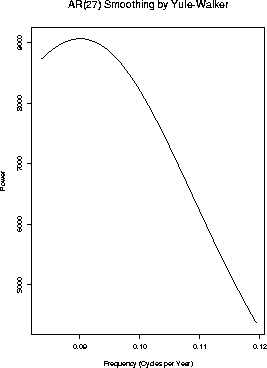
- Prewhitening by the AR(27) model selected by the use of AIC:
- Prewhitening by a high order AR(1000).




Richard Lockhart
2001-09-30
![]() as an estimate of
as an estimate of ![]() . We
have already shown that
. We
have already shown that
![]() . For
normal data the real and imaginary parts of
. For
normal data the real and imaginary parts of ![]() have normal distributions.
Both have mean 0. The variances are
have normal distributions.
Both have mean 0. The variances are






![]() may be simplified by using geometric series
to do the inside sums over
may be simplified by using geometric series
to do the inside sums over ![]() . The result is a coefficient of
. The result is a coefficient of ![]() which is bounded (bounded by
which is bounded (bounded by
![]() for instance. Then
since
for instance. Then
since

![]() can be mimicked to show that the two variances each converge to
can be mimicked to show that the two variances each converge to
![]() . It follows that the vector
. It follows that the vector
![]() converges to a bivariate standard normal.
The squared length of this vector then converges in distribution to
the squared length of a standard bivariate normal which is exactly
converges to a bivariate standard normal.
The squared length of this vector then converges in distribution to
the squared length of a standard bivariate normal which is exactly
![]() or exponential with mean 2.
or exponential with mean 2.
![]() converges in distribution to an
exponential random variable with mean
converges in distribution to an
exponential random variable with mean ![]() . In particular,
. In particular,
![]() is not a consistent estimator of
is not a consistent estimator of ![]() .
.
![]() is smooth in the neighbourhood of some
is smooth in the neighbourhood of some ![]() then we
can take estimates of
then we
can take estimates of ![]() at a number of points nearby to
at a number of points nearby to
![]() and average them somehow. Averaging will reduce the variance
though it will introduce bias usually because the things being averaged all
have different expected values.
and average them somehow. Averaging will reduce the variance
though it will introduce bias usually because the things being averaged all
have different expected values.











