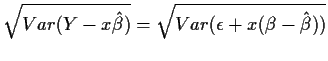Given data
![]() our goal will be to guess, or
forecast,
our goal will be to guess, or
forecast, ![]() or more generally
or more generally ![]() . There are a variety
of ad hoc methods as well as a variety of statistically
derived methods. I illustrate the ad hoc methods with the
exponentially weighted moving average (EWMA). In this case
we simply take
. There are a variety
of ad hoc methods as well as a variety of statistically
derived methods. I illustrate the ad hoc methods with the
exponentially weighted moving average (EWMA). In this case
we simply take
Statistically based methods concentrate on some measure of the size of
![]() ;
the mean squared prediction error
;
the mean squared prediction error
![]() is
the most common.
is
the most common.
In general
![]() must be some function
must be some function
![]() .
The mean squared prediction error can be seen by conditioning
on the data to be minimized by
.
The mean squared prediction error can be seen by conditioning
on the data to be minimized by
When ![]() is large the computation of these forecasts is difficult
in general. There are some shortcuts, however.
is large the computation of these forecasts is difficult
in general. There are some shortcuts, however.
Forecasting AR(![]() ) processes
) processes
When the process is an AR the computation of the conditional
expectation is easier:
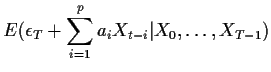 |
|||
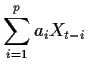 |
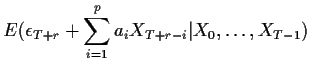 |
|||
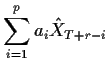 |
Notice the the forecast into the future uses current values
where these are available and forecasts already calculated
for the other ![]() 's.
's.
Forecasting ARMA(![]() ) processes
) processes
An ARMA(![]() ) can be inverted to be an infinite order AR
process. We could then use the method just given for the
AR except that now the formula actually mentions values of
) can be inverted to be an infinite order AR
process. We could then use the method just given for the
AR except that now the formula actually mentions values of ![]() for
for ![]() . In practice we simply truncate the series and
ignore the missing terms in the forecast, assuming that the
coefficients of these omitted terms are very small. Remember
each term is built up out of a geometric series for
. In practice we simply truncate the series and
ignore the missing terms in the forecast, assuming that the
coefficients of these omitted terms are very small. Remember
each term is built up out of a geometric series for
![]() with
with
![]() .
.
A more direct method goes like this:
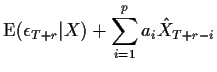 |
|||
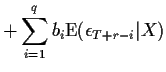 |
Whenever the time index on an epsilon is ![]() or more the conditional
expectations are 0. For
or more the conditional
expectations are 0. For ![]() we need to guess the value
of
we need to guess the value
of
![]() . The same recurtion can be re-arranged to
help compute
. The same recurtion can be re-arranged to
help compute
![]() for
for
![]() , at least
approximately:
, at least
approximately:
As we discussed in the section on estimation these computed
estimates of the epsilon's can be improved by backcasting the
values of
![]() for negative
for negative ![]() and then forecasting and
backcasting, etc.
and then forecasting and
backcasting, etc.
Forecasting ARIMA(![]() ) series
) series
If
![]() and
and ![]() is ARIMA(
is ARIMA(![]() ) then we:
compute
) then we:
compute ![]() , forecast
, forecast ![]() and reconstruct
and reconstruct ![]() by
undoing the differencing. For
by
undoing the differencing. For ![]() for example we
just have
for example we
just have
Forecast standard errors
You should remind yourself that the computations of conditional
expectations we have just made used the fact that the ![]() 's and
's and
![]() 's are constants - the true parameter values. In fact we
then replace the parameter values with estimates. The quality of
our forecasts will be summarized by the forecast standard error:
's are constants - the true parameter values. In fact we
then replace the parameter values with estimates. The quality of
our forecasts will be summarized by the forecast standard error:
![$\displaystyle \sqrt{{\rm E}[(X_t-{\hat X}_t)^2]} \, .
$](img55.gif)
If
![]() then
then
![]() so that our forecast standard error is just the variance of
so that our forecast standard error is just the variance of
![]() .
.
Consider first the case of an AR(1) and one step ahead forecasting:
For forecasts further ahead in time we have
Turn now to a general ARMA(![]() ). Rewrite the process as the infinite
order AR
). Rewrite the process as the infinite
order AR
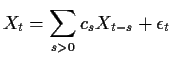
Parallel to the AR(1) argument we see that
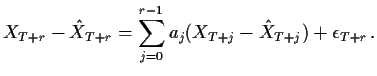
A simpler approach is to write the process as an infinite order MA:
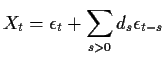
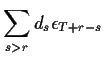 |
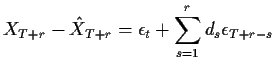
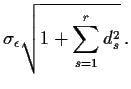
Finally consider forecasting the ARIMA(![]() ) process
) process
![]() where
where ![]() is ARMA(
is ARMA(![]() ).
The forecast errors in
).
The forecast errors in ![]() can clearly be written as a linear combination of
forecast errors for
can clearly be written as a linear combination of
forecast errors for ![]() permitting the forecast error in
permitting the forecast error in ![]() to be written as
a linear combination of the underlying errors
to be written as
a linear combination of the underlying errors
![]() . As an example consider
first the ARIMA(0,1,0) process
. As an example consider
first the ARIMA(0,1,0) process
![]() . The forecast of
. The forecast of
![]() is just 0 and so the forcast of
is just 0 and so the forcast of ![]() is just
is just
The forecast error is
Software
The S-Plus function arima.forecast can do the forecasting.
Comments
I have ignored the effects of parameter estimation throughout. In ordinary least squares
when we predict the ![]() corresponding to a new
corresponding to a new ![]() we get a forecast standard error
of
we get a forecast standard error
of