be the population standard deviation
for control rats and 
be the treatment population standard
deviation. Then to test 
against the one
sided alternative 
we compute 
and
get upper tail P-values from F tables with 19 and 22 degrees of
freedom. We get F = 2.85 and P just a bit bigger than 0.01 so that we
conclude that the treatment population is more variable. (While the
question asks a one-tailed question it is not entirely clear to me that the
tail was not chosen after seeing the data; if so you should double the
P-value. The conclusion is not really changed.)
has an F distribution so that
The right hand inequality holds if and only if
Similarly, the first inequality can be rearranged to be
so that the range between these two limits is a level 
confidence
interval for 
. For the data we have
and 
. The critical point
while to find the lower tail critical point
we use 
.
The interval is then 0.00549/(0.0258*9.28) to (9.28)(0.00549)/0.0258.
Note that some people may have put 
on top.
-
. Use 
and the fact that summing over
j just multiplies by J to get
. -
.
The variance of any average of J independent quantities each with
variance 
is just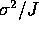 
so we get
. -
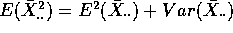which, using (a) and the rule in (b) is
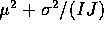. - We have
.
Expand out the square and use the fact that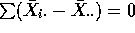 
to see that
Take expected values and put in the results of (b) and (c) to get
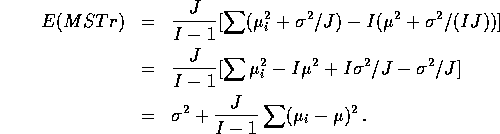
- Under
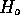the second of these terms is 0 so 
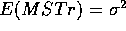while under the alternative the second term is positive so that
.
we have 
, 
,
and all the other 
so that the confidence interval for
is 
(where we use the level 
for a 95% confidence
interval). For the other intervals it is the values of the 
which
change. They are (1,0,-1), (0,1,-1) and (0.5,0.5,-1) respectively.
Only the contrast 
is judged significantly different from 0.
(Note the use of 
not 
; these are 95% confidence
intervals.)
and 
. Subtracting we get
so the the SSE
for the y's is 
times the SSE for the x's. Similarly we have
so that the new SSTr is times the old SSTr.
The factors then cancel out in the formula for the F statistic so
that the new F statistic is exactly equal to the old F statistic.
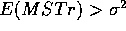- The two samples are now
for 
and
for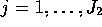 
. The two sample variances are
and
.
Then the pooled estimate of is
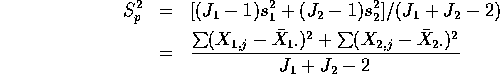
which is just
which is in turn just the MSE.
- The pooled statistic squared is just
Now write
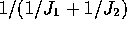as 
to see that
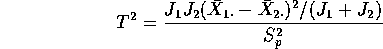
Now examine the Treatment Sum of Squares. First note that
. Use this to see that the Treatment Sum of Squares
is given by
which simplifies to
This last is the numerator of
.
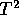