STAT 330: 95-3

Assignment 3 Solutions

1. Q 59, Chapter 9. Let and be the mean dry densities for soil samples gathered by the two methods (in practical terms I wonder what the population of soil was). This is a straightforward application of the two independent samples confidence interval methodology. We have , , and . I count and . The pooled estimate of the standard deviation is then which is 3.70, leading to the pooled estimate of the standard error of being

   

   Thus use of the two sample t based confidence interval (on 33 degrees of freedom) gives the interval or -0.19 to 5.29. Using the interval which does not pool seems inadvisable here since one of the two sample sizes is small. However, the unpooled estimated standard error of the difference in means is

   

   Thus this interval, using the normal multiplier 1.96 is -0.1 to 5.2. (Aside: there is an approximation due to Welch or Satterthwaite to the distribution of the t-statistic which leads to using the large sample statistic but with a t multiplier with degrees of freedom being

   

   where

   

   which comes to 20.16 degrees of freedom leading to the multiplier 2.085 and the interval which runs from -0.22 to 5.32.)

2. Chapter 9, Q 60: Another 2 sample unpaired t problem with no real evidence that the two population standard deviations are unequal so we use the two sample unpaired t-test (two tailed). We get and use 16 degrees of freedom leading to the test statistic t = 6.38. The P value from this statistic is minute - .
3. Chapter 9, Q 66: Let be the probability that an egg survives at 11 degrees and the probability that an egg survives at 30 degrees. The null hypothesis is that these two probabilities are the same while the alternative appears to be that they are not the same. Under the null hypothesis we estimate the common value by . The test statistic is

   

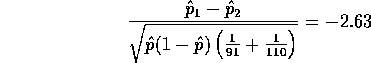
   leading to a P-value of 0.85% which is strong evidence against equal probabilities.

4. Chapter 9, Q 70: This is another problem with two independent samples. It might have been paired if there were 8 hospitals involved with one room of each type in each hospital. I don't think that is what is intended here. However: if you did use a paired test you get valid conclusions but only 7 degrees of freedom rather than 14 as in the unpaired case. I get a P-value of 35% and conclude that there is little solid evidence of a difference. If I found out that the two hospitals were of different kinds then I would not know whether the difference in bacteria counts was due to carpeting or to the different natures of the hospitals - this is called confounding. In general confounding can be avoided only by randomization which requires a controlled experiment (and not an observational study) in which the experimenter controls which rooms are carpeted and chooses those rooms at random.
5. Chapter 9, Q 74: The interval is

   

   or . The subscript 1 refers to foreign drivers.

6. Chapter 9, Q 75:
   1. A standard two sample problem with 2 independent samples. The z statistic is

      

      Since the sample sizes are equal the pooled and unpooled versions are identical. The statistic works out to -6.4 which is overwhelming evidence that the two filling operations produce different mean weights.

   2. This is a one sample problem testing 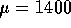against the alternative that it is more than 1400. The statistic is

      

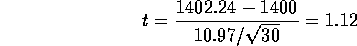
      yielding a one sided P-value of 13.6% from a t distribution on 29 degrees of freedom or of 13.1% from the normal curve showing that it doesn't really matter which you use. This is only very weak evidence against the null hypothesis which wold be accepted.

7. In 1879, over the period from June 5 to July 2, Michelson carried out a number of measurements of the speed of light. The first 20 measurements and last 20 measurements (minus 299000 km/sec) and several summary statistics are recorded below.

   First 20 Second 20 Difference

   850 890 -40

   740 840 -100

   900 780 120

   1070 810 260

   930 760 170

   850 810 40

   950 790 160

   980 810 170

   980 820 160

   880 850 30

   1000 870 130

   980 870 110

   930 810 120

   650 740 -90

   760 810 -50

   810 940 -130

   1000 950 50

   1000 800 200

   960 810 150

   960 870 90

   Average=909 Average=831.5 Average=77.5

   SD=104.9 SD=54.2 SD=109.8

   Has the bias of the measurements changed between the first 20 and the last 20?

   Solution

   This is not a paired data problem; I just calculated the differences to confuse. There is no natural pairing between the first measurement and the first of the last 20. Taking the two independent samples model the question is whether the mean of the first 20 is the same as the mean of the last 20. The idea is that each mean is the true speed of light plus a bias and so the means are equal if and only if the biases are the same.

   It is not obvious that the standard deviations are unchanged (and the statistical evidence is that the standard deviation has indeed changed). We thus do not pool the estimates of the standard deviations and our test statistic is

   

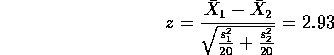
   (Numerically, though, since the two sample sizes are the same the statistic has the same value as the two sample t statistic using a pooled variance estimate.) Looking in normal tables and carrying out a 2 tailed test we get a P value of 0.3% and conclude that the bias has indeed changed.

   Although the data are not paired the paired comparisons t-test is still valid and the resulting statistic is 3.16 on 19 degrees of freedom yielding a P-value of 0.5% which leads to the same conclusion. The previous calculation based on the unpaired method would have had 38 degrees of freedom if the assumption of equal variances were valid and an indistinguishable P-value.

8. Annual records were kept in the Prussian army for the number of deaths by horsekick.

   Year Number of Year Number of

   deaths deaths

   1875 3 1885 5

   1876 5 1886 11

   1877 7 1887 15

   1070 9 1888 6

   1879 10 1889 11

   1880 18 1890 17

   1881 6 1891 12

   1882 14 1892 15

   1883 11 1893 8

   1884 9 1894 4

   Total 92 104

   1. Use a Poisson model and obtain a 95% confidence interval for the long run average mean number of deaths per year.

      I did this in class and obtained two intervals: the first, for the parameter 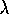(which is the annual rate) is

      

      and the second is the interval for 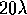based on solving a quadratic

      

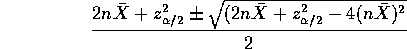
      This last interval translates to one for 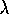by dividing by n=20 to get

      

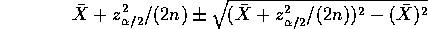
      or

      

      which is about the same width but centred slightly differently. The difference is negligible.

   2. Develop a test of the hypothesis that there has been no change in this underlying death rate over the time period in question as follows. Let N be the number of deaths in the first 10 years and M the number in the second 10 years. If the Poisson model with constant death rate is credible then M and N have the same mean. What is the standard error of N-M in terms of the Poisson parameter? How can you estimate this standard error? How can you use this to test the hypothesis that there is no change in mean?

      If 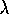is the per year rate and this is the same for all 20 years then both N and M have Poisson distributions with parameters . Then and the natural test statistic is

      

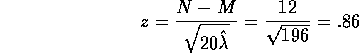
      leading to a (two sided) P-value of 39% which is not significant.