STAT 330: 98-1: Midterm Solutions

Midterm, 23 February 1998Instructor: Richard Lockhart

1. The table below shows, in the column labelled BEFORE, 15 measurements of the speed of sound in air. After taking the measurements the machine is recalibrated and a further 15 measurements are taken; these are in the column labelled after. Differences between the before and after measurements are in the last column. The table gives means and standard deviations as well.

   Mmnt # BEFORE AFTER DIFFERENCE

   1 331.32 331.59 0.27

   2 331.59 331.43 -0.16

   3 331.01 331.85 0.84

   4 331.53 331.63 0.10

   5 330.69 331.66 0.97

   6 330.95 331.21 0.26

   7 331.13 331.75 0.62

   8 330.69 332.14 1.45

   9 331.84 331.36 -0.48

   10 330.88 331.82 0.94

   11 331.41 330.84 -0.57

   12 331.09 331.80 0.71

   13 331.20 331.84 0.64

   14 330.80 331.15 0.35

   15 330.53 331.40 0.87

   Mean 331.111 331.565 0.454

   SD 0.374 0.335 0.564

   1. Give a 95% confidence interval for the true speed of sound in air based on the measurements before recalibration. [ 4 marks]

      Solution: This is a one sample t type confidence interval problem. The assumption is that the measurements are a sample from a normal population whose mean is the true speed of sound in air. The interval is

      

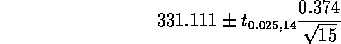
      or

      

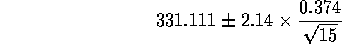
   2. Has the precision of the measurements been changed by recalibration? [4 marks]

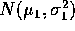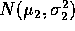      Solution: The question is whether or not has changed between the two sets. You have from a population (the BEFORE) measurements and from a population (the AFTER) measurements. You want to test 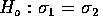against a two sided alternative. The test statistic is

      

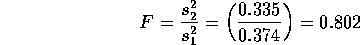
      The critical points for a 10% level test are and and we must accept this null hypothesis. There is little evidence of a change in precision following recalibration.

   3. Has the bias of the measurements been changed by recalibration? [4 marks]

      Solution: This question asks for a test of with a two sided alternative. Since the recalibration happens between the first 15 measurements and the second 15 there is no sense in which the data are really paired. The pooled estimate of is

      

      leading to

      

      This leads to a P value (using t tables with 28 degrees of freedom) of about 0.0016. So there is very clear evidence that the bias has changed after recalibration.

2. Two independent surveys of 400 male and 300 female voters in Calgary show support for the Reform Party at 49% among men and 37% among women. Is there a difference in support levels between male and female voters in Calgary? [4 marks]

   Solution: This is a two sample test of against a two sided alternative. The pooled estimate of p under the null hypothesis is

   

   and then

   

   which leads to a P value of 2(1-.9992)=0.0016. There is very strong evidence of a difference between men and women in support for Reform in Calgary.

3. I have two possible routes to work. I intend to carry out the following experiment. I will drive each route n times. On each trip I will record how long the trip takes. I expect the standard deviation for the time taken to be around 4 minutes on either route. I plan to analyze the data using a test carried out with fixed level 0.05. As a time fanatic I want to run a risk of no more that 1% of not detecting a difference in average travel times of 1 minute between the routes.
   1. How many times should I try each route? [2 marks]

      Solution: This a two sample two sided test and we will see that the solution is a large sample size so that the normal distribution formulas will be just fine. On the bottom of page 351 we see that

      

      or just 589 trips on each route. This sort of accuracy will require 4 or 5 years of experimentation!

   2. Now suppose that the answer to the first part of this question is 20. I am considering three plans for organizing my 40 trips. Plan A has me take route 1 the next 20 times and then route 2 the 20 times after that. Plan B has me alternate: a trip on route 1 then one on route 2 then route 1 again and so on. Plan C has me make up 40 tickets, 20 of which are marked route 1 and each time I go to make a trip selecting another ticket at random. Assume I come to work Monday, Tuesday, Wednesday and Friday each week. Which plan would a statistician recommend and why? Your answer should include a 1 sentence specific criticism of the plans not recommended. Your answer will be about 4 sentences long. [2 marks]

      Solution: Plan A is susceptible to a change in traffic patterns over time. If traffic levels go up over time the experiment will be biased in favour of the route I try first. Plan B is susceptible to day of the week effects - route 1 will be Monday and Wednesday. Since traffic is heaviest on Friday the design would be biased in favour of route 1. The randomization balances out (probably) any other factors which might affect the length of my trip (day of week, time of day, time of year, weather, ...).

4. You have a sample from the density for x > 0 and for .
   1. Find the MLE of . [3 marks]

      Solution: The likelihood is

      

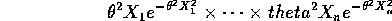
      which simplifies to

      

      Take logs to get the log likelihood:

      

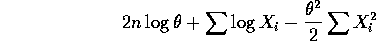
      The derivative with respect to is

      

      Set this equal to 0 and solve to get

      

   2. The expected value of is

      

      What integral do you have to do to show this? You need not do the integral! [1 mark]

      Solution:

      

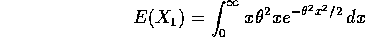
   3. What is the method of moments estimate of ? [1 mark]

      Solution: Set or

      

      and solve for to get