STAT 330: 96-3

Midterm, 18 October 1996Instructor: Richard Lockhart

Instructions: This is an open book test. You may use notes, text, other books and a calculator. Your presentations of statistical analysis will be marked for clarity of explanation. I expect you to explain what assumptions you are making and to comment if those assumptions seem unreasonable. The exam is out of 25.

  1. A simple random sample of 900 adult British Columbians is drawn. Each is asked how much beer he or she drinks per day.

    1. Assume that the 900 answers average 600 ml with a standard deviation of 750 ml. Give a 90% confidence interval for the average daily beer consumption of all adult British Columbians. [5 marks]
    2. Suppose that a year earlier a survey of 1600 voters had given an average of 550 ml with a standard deviation of 800 ml. Has daily beer consumption increased over the year? [5 marks]
    3. In the more recent survey (the one of 900 people) 300 report not drinking anything while in the earlier survey the corresponding figure was 400 people. Has there been a change in the fraction of all adults who do not drink? [5 marks]
    4. Briefly (2 or 3 sentences) criticize the assumptions used in the previous three parts and comment on the realism of the description of outcome of the survey. [1 mark]

  2. When you toss a thumbtack it can either land point up or tipped over. I have been told that the probability of landing point up is around 0.7 for a certain brand of tack. How many times should I toss the tack to be 99% sure that I will reject the hypothesis that the probability of landing point up is 0.5 at the level 5%? [3 marks]
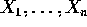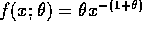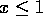  3. You have a sample tex2html_wrap_inline36 from the density tex2html_wrap_inline38 for x > 1 and tex2html_wrap_inline42 for tex2html_wrap_inline44 . Find the MLE of tex2html_wrap_inline46 . [3 marks]
  4. Suppose you have two independent samples, tex2html_wrap_inline48 and tex2html_wrap_inline50 from two populations with means tex2html_wrap_inline52 and tex2html_wrap_inline54 and variances tex2html_wrap_inline56 and tex2html_wrap_inline58 . Let tex2html_wrap_inline60 and tex2html_wrap_inline62 be the two sample variances. Under the assumption that tex2html_wrap_inline64 I showed in class that tex2html_wrap_inline66 is an unbiased estimate of tex2html_wrap_inline68 . The variance of tex2html_wrap_inline70 is tex2html_wrap_inline72 Show that tex2html_wrap_inline74 is an unbiased estimate of this variance and calculate the bias of tex2html_wrap_inline76 (as an estimate of this tex2html_wrap_inline78 ) if we do not assume that tex2html_wrap_inline64 . [3 marks]


Richard Lockhart
Wed Feb 11 10:38:12 PST 1998