ENSC 220
ELECTRIC CIRCUITS I

Lab #4: RLC Circuits

OBJECTIVE:
You will study a series RLC circuit from both a time-domain and frequency-domain perspective in order to investigate topics such as: damping, overshoot, rise time, frequency of oscillation, settling time, resonance, bandwidth and Q.

PREPARATION:
Read Lab Handbook

  • ``Inductors, Inductive Devices and Cores''
  • Appendix II ``Mathematical Formulae''
  • Appendix III ``Pulse Parameter Definitions''

    EQUIPMENT:

  • Oscilloscope, Tektronix 2245, 2235, TAS465, or similar 2 channel scope
  • 100 uH inductor (supplied in parts bag previously distributed)
  • Your own made inductor from Lab #3
  • 1 capacitor in the range 100pF - 10nF
  • Function generator
  • Breadboard
  • Resistors.

    NOTES:

  • Ensure good contact on inductor taps by tinning with solder.
  • Calculate values for Runder and Rover prior to showing up in the lab, or learn how to do this in a tutorial.

    METHOD:

    TIME-DOMAIN RESPONSE:

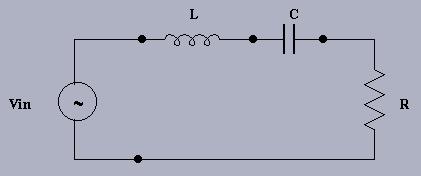
    Use one capacitor (suggest C = 100pF - 10nF) and two different inductors: the one that you made for Lab #3 and a 100uH inductor that will be supplied to you (try to calibrate your inductor close to 100uH for comparison purposes). Use two different resistors: one that demonstrates under-damping (Runder) and one producing an over-damped response (Rover). Sketch the step response for the output voltage Vout taken across the resistor, R, in each case. Measure (if possible): overshoot, rise time, settling time, and frequency of oscillation.

    Click here for the DERIVATION of the natural frequencies.

    FREQUENCY-DOMAIN RESPONSE:

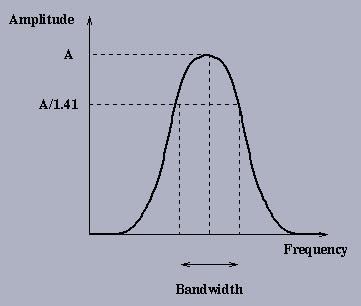
    Apply a sinusoidal voltage to the input. Choose several appropriate frequencies and measure the amplitude (with respect to the input amplitude) ratio and phase difference (with respect to the input sinusoid) at each frequency. Plot the frequency response (amplitude vs. frequency) for each case (Runder and Rover) as shown in the figure.

    For both Runder and Rover cases, determine from these plots:
    1. Resonant frequency (wr)
    2 Bandwidth (BW)
    3. Quality factor (Q, where Q = wr/BW).

    Note that a ``high Q'' circuit has a very narrow bandwidth with respect to its resonant frequency.

    DISCUSSION:
    For both Runder and Rover cases, calculate:
    1. Resonant frequency: wr = 1/sqrt(LC)
    2. Bandwidth: BW = R/L
    3. Quality factor: Q = sqrt(L/C)/R.
    Compare these to the values determined from your graphs.

    If a series RC, RL, or RLC circuit was given to you in a black box (with access only to the two input terminals) how could you determine the component values? Try to identify several circuits.

    Last modified: Fri Nov 13 18:19:35 PST 1998.