The Penalized Least Squares Estimate

The TPSPLINE Procedure

The Penalized Least Squares Estimate

Penalized least squares estimates provide a way to balance fitting the data closely and avoiding excessive roughness or rapid variation. A penalized least squares estimate is a surface that minimizes the penalized least squares over the class of all surfaces satisfying sufficient regularity conditions.

Define x_i as a d-dimensional covariate vector, z_i as a p-dimensional covariate vector, and y_i as the observation associated with (x_i, z_i). Assuming that the relation between z_i and y_i is linear but the relation between x_i and y_i is unknown, you can fit the data using a semiparametric model as follows:

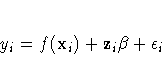
$y_i=f({x}_i)+{z}_i{{\beta}} +\epsilon_i$

where f is an unknown function that is assumed to be reasonably smooth, $\epsilon_i, i=1, ... ,n$ are independent, zero-mean random errors, and ${{\beta}}$ is a p-dimensional unknown parametric vector.

This model consists of two parts. The ${z}_i{{\beta}}$ is the parametric part of the model, and the z_i are the regression variables. The f(x_i) is the nonparametric part of the model, and the x_i are the smoothing variables.

The ordinary least squares method estimates f(x_i) and ${{\beta}}$ by minimizing the quantity:

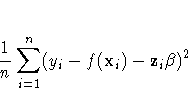
$\frac{1}n \sum^n_{i=1}(y_i-f({x}_i)-{z}_i{{\beta}})^2$

However, the functional space of f(x) is so large that you can always find a function f that interpolates the data points. In order to obtain an estimate that fits the data well and has some degree of smoothness, you can use the penalized least squares method.

The penalized least squares function is defined as

$S_\lambda(f)=\frac{1}n \sum^n_{i=1} (y_i-f({x}_i)-{z}_i{{\beta}})^2 + \lambda J_2(f)$

where J₂(f) is the penalty on the roughness of f and is defined, in most cases, as the integral of the square of the second derivative of f.

The first term measures the goodness of fit and the second term measures the smoothness associated with f. The $\lambda$ term is the smoothing parameter, which governs the tradeoff between smoothness and goodness of fit. When $\lambda$ is large, it heavily penalizes estimates with large second derivatives. Conversely, a small value of $\lambda$ puts more emphasis on the goodness of fit.

The estimate $f_\lambda$ is selected from a reproducing kernel Hilbert space, and it can be represented as a linear combination of a sequence of basis functions. Hence, the final estimates of f can be written as

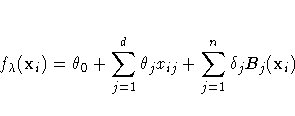
$f_\lambda({x}_i)=\theta_0+\sum_{j=1}^d \theta_j x_{ij}+\sum_{j=1}^n \delta_j B_j({x}_i)$

where B_j is the basis function, which depends on where the data x_j is located, and $\theta_j$ and $\delta_j$ are the coefficients that need to be estimated.

For a fixed $\lambda$ , the coefficients $({\theta, \delta, \beta})$ can be estimated by solving an n×n system.

The smoothing parameter can be chosen by minimizing the generalized cross validation (GCV) function.

If you write

$\hat{y}={A}(\lambda) {y}$

then $A(\lambda)$ is referred to as the hat or smoothing matrix, and the GCV function $V(\lambda)$ is defined as

$V(\lambda)=\frac{(1/n)||({I}-{A}(\lambda)){y}||^2} {[(1/n)tr({I}-{A}(\lambda))]^2}$

Chapter Contents
Previous
Next
Top