Modeling Assumptions and Notation
PROC NLMIXED operates under the following general framework for
nonlinear mixed models. Assume that you have an observed data vector
yi for each of i subjects, i = 1, ... ,s. The yi are
assumed to be independent across i, but within-subject covariance
is likely to exist because each of the elements of yi are
measured on the same subject. As a statistical mechanism for
modeling this within-subject covariance, assume that there exist latent
random-effect vectors ui of small dimension (typically one or
two) that are also independent across i. Assume also that an
appropriate model linking yi and ui exists, leading to the
joint probability density function
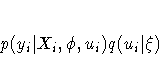
where Xi is a matrix of observed explanatory variables and  and
and  are vectors of unknown parameters.
are vectors of unknown parameters.
Let  and assume that it is of dimension n.
Then inferences about
and assume that it is of dimension n.
Then inferences about  are based on the marginal likelihood
function
are based on the marginal likelihood
function
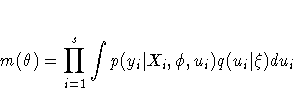
In particular, the function
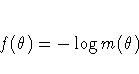
is minimized over  numerically in order to estimate
numerically in order to estimate
 , and the inverse Hessian (second derivative) matrix at the
estimates provides an approximate variance-covariance matrix for the
estimate of
, and the inverse Hessian (second derivative) matrix at the
estimates provides an approximate variance-covariance matrix for the
estimate of  . The function
. The function  is referred to both
as the negative log likelihood function and as the objective function
for optimization.
is referred to both
as the negative log likelihood function and as the objective function
for optimization.
As an example of the preceding general framework, consider the
nonlinear growth curve example in the "Getting Started"
section. Here, the conditional distribution  is normal with mean
is normal with mean
-
[(b1 + ui1)/(1 + exp[-(dij - b2)/ b3])]
and variance  ; thus
; thus  .Also, ui is a scalar and
.Also, ui is a scalar and  is normal with mean 0 and
variance
is normal with mean 0 and
variance  ; thus
; thus  .
.The following additional notation is also found in this chapter.
The quantity  refers to the parameter vector at the
kth iteration, the function
refers to the parameter vector at the
kth iteration, the function  refers to the gradient
vector
refers to the gradient
vector  , and the matrix
, and the matrix  refers to the
Hessian
refers to the
Hessian  . Other symbols are used to denote
various constants or option values.
. Other symbols are used to denote
various constants or option values.
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
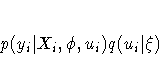
![]() and assume that it is of dimension n.
Then inferences about
and assume that it is of dimension n.
Then inferences about ![]() are based on the marginal likelihood
function
are based on the marginal likelihood
function
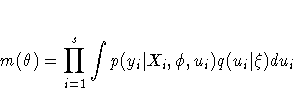
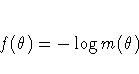
![]() is normal with mean
is normal with mean
![]() refers to the parameter vector at the
kth iteration, the function
refers to the parameter vector at the
kth iteration, the function ![]() refers to the gradient
vector
refers to the gradient
vector ![]() , and the matrix
, and the matrix ![]() refers to the
Hessian
refers to the
Hessian ![]() . Other symbols are used to denote
various constants or option values.
. Other symbols are used to denote
various constants or option values.