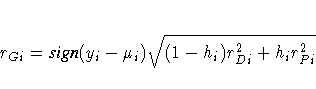Residuals

Chapter Contents

The GENMOD Procedure

Residuals

The GENMOD procedure computes three kinds of residuals. The raw residual is defined as

$r_i = y_i - \mu_i$

where y_i is the ith response and $\mu_i$ is the corresponding predicted mean.

The Pearson residual is the square root of the ith contribution to the Pearson's chi-square.

$r_{Pi} = (y_i - \mu_i) \sqrt{ \frac{w_i}{V(\mu_i)} }$

Finally, the deviance residual is defined as the square root of the contribution of the ith observation to the deviance, with the sign of the raw residual.

$r_{Di} = \sqrt{d_i}({sign}(y_i - \mu_i))$

The adjusted Pearson, deviance, and likelihood residuals are defined by Agresti (1990), Williams (1987), and Davison and Snell (1991). These residuals are useful for outlier detection and for assessing the influence of single observations on the fitted model.

For the generalized linear model, the variance of the ith individual observation is given by

$v_i = \frac{\phi V(\mu_i)}{w_i}$

where $\phi$ is the dispersion parameter, w_i is a user-specified prior weight (if not specified, w_i=1), $\mu_i$ is the mean, and $V(\mu_i)$ is the variance function. Let

$w_{ei} = v_i^{-1}(g^'(\mu_i))^{-2}$

for the ith observation, where $g^'(\mu_i)$ is the derivative of the link function, evaluated at $\mu_i$ .Let W_e be the diagonal matrix with w_ei denoting the ith diagonal element. The weight matrix W_e is used in computing the expected information matrix.

Define h_i as the ith diagonal element of the matrix

W_e^(1/2) X (X' W_e X)^-1 X' W_e^(1/2)

The Pearson residuals, standardized to have unit asymptotic variance, are given by

$r_{Pi} = \frac{y_i - \mu_i}{\sqrt{v_i(1 - h_i)}}$

The deviance residuals, standardized to have unit asymptotic variance, are given by

$r_{Di} = \frac{{sign}(y_i - \mu_i) \sqrt{d_i}} {\sqrt{\phi(1 - h_i)}}$

where d_i is the square root of the contribution to the total deviance from observation i, and sign $(y_i - \mu_i)$ is 1 if $y_i - \mu_i$ is positive and -1 if $y_i - \mu_i$ is negative. The likelihood residuals are defined by

$r_{Gi} = {sign}(y_i - \mu_i) \sqrt{(1 - h_i)r_{Di}^2 + h_i r_{Pi}^2}$

Chapter Contents
Previous
Next
Top