Example 5.8: Chemical Equilibrium
The following example is used in many test libraries
for nonlinear programming and was taken originally
from Bracken and McCormick (1968).
The problem is to
determine the composition of a mixture of various
chemicals satisfying its chemical equilibrium state.
The second law of thermodynamics implies that a
mixture of chemicals satisfies its chemical equilibrium
state (at a constant temperature and pressure) when
the free energy of the mixture is reduced to a minimum.
Therefore the composition of the chemicals satisfying
its chemical equilibrium state can be found by minimizing
the function of the free energy of the mixture.
Notation:
- m number of chemical elements in the mixture
- n number of compounds in the mixture
- xj number of moles for compound j, j = 1, ... ,n
-
 total number of moles in the mixture
total number of moles in the mixture
- aij number of atoms of element i in a molecule
of compound j
- bi the atomic weight of element i in the mixture
Constraints for the Mixture:
- The number of moles cannot be negative,
-
xj > 0 , j = 1, ... ,n
- There are m mass balance relationships,
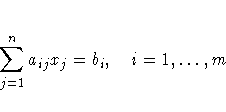
Objective Function: Total Free Energy of Mixture
![f(x) = \sum_{j=1}^n x_j [c_j + ln({x_j \over s})]](images/nlpeq213.gif)
with
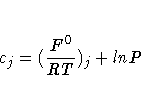
where  is the model standard free
energy function for the jth compound (that is found
in tables) and P is the total pressure in atmospheres.
is the model standard free
energy function for the jth compound (that is found
in tables) and P is the total pressure in atmospheres.
Minimization Problem:
Determine the parameters xj that minimize the
objective function f(x) subject to the nonnegativity
and linear balance constraints.
Numeric Example:
Determine the equilibrium composition of compound
 at temperature
T= 3500oK and pressure P= 750 psi.
at temperature
T= 3500oK and pressure P= 750 psi.
| | aij |
| | i=1 | i=2 | i=3 |
| j | Compound | (F0 / RT)j | cj | H | N | O |
| 1 | H | -10.021 | -6.089 | 1 | | |
| 2 | H2 | -21.096 | -17.164 | 2 | | |
| 3 | H2O | -37.986 | -34.054 | 2 | | 1 |
| 4 | N | -9.846 | -5.914 | | 1 | |
| 5 | N2 | -28.653 | -24.721 | | 2 | |
| 6 | NH | -18.918 | -14.986 | 1 | 1 | |
| 7 | NO | -28.032 | -24.100 | | 1 | 1 |
| 8 | O | -14.640 | -10.708 | | | 1 |
| 9 | O2 | -30.594 | -26.662 | | | 2 |
| 10 | OH | -26.111 | -22.179 | 1 | | 1 |
Example Specification:
proc nlp tech=tr pall;
array c[10] -6.089 -17.164 -34.054 -5.914 -24.721
-14.986 -24.100 -10.708 -26.662 -22.179;
array x[10] x1-x10;
min y;
parms x1-x10 = .1;
bounds 1.e-6 <= x1-x10;
lincon 2. = x1 + 2. * x2 + 2. * x3 + x6 + x10,
1. = x4 + 2. * x5 + x6 + x7,
1. = x3 + x7 + x8 + 2. * x9 + x10;
s = x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10;
y = 0.;
do j = 1 to 10;
y = y + x[j] * (c[j] + log(x[j] / s));
end;
run;
Displayed Output:
The iteration history does not show any problems.
Output 5.8.1: Iteration History
|
| PROC NLP: Nonlinear Minimization |
| Iteration |
|
Restarts |
Function
Calls |
Active
Constraints |
|
Objective
Function |
Objective
Function
Change |
Max Abs
Gradient
Element |
Lambda |
Trust
Region
Radius |
| 1 |
|
0 |
2 |
3 |
' |
-47.33412 |
2.2790 |
6.0765 |
2.456 |
1.000 |
| 2 |
|
0 |
3 |
3 |
' |
-47.70043 |
0.3663 |
8.5592 |
0.908 |
0.418 |
| 3 |
|
0 |
4 |
3 |
|
-47.73074 |
0.0303 |
6.4942 |
0 |
0.359 |
| 4 |
|
0 |
5 |
3 |
|
-47.73275 |
0.00201 |
4.7606 |
0 |
0.118 |
| 5 |
|
0 |
6 |
3 |
|
-47.73554 |
0.00279 |
3.2125 |
0 |
0.0168 |
| 6 |
|
0 |
7 |
3 |
|
-47.74223 |
0.00669 |
1.9552 |
110.6 |
0.00271 |
| 7 |
|
0 |
8 |
3 |
|
-47.75048 |
0.00825 |
1.1157 |
102.9 |
0.00563 |
| 8 |
|
0 |
9 |
3 |
|
-47.75876 |
0.00828 |
0.4165 |
3.787 |
0.0116 |
| 9 |
|
0 |
10 |
3 |
|
-47.76101 |
0.00224 |
0.0716 |
0 |
0.0121 |
| 10 |
|
0 |
11 |
3 |
|
-47.76109 |
0.000083 |
0.00238 |
0 |
0.0111 |
| 11 |
|
0 |
12 |
3 |
|
-47.76109 |
9.609E-8 |
2.733E-6 |
0 |
0.00248 |
| Optimization Results |
| Iterations |
11 |
Function Calls |
13 |
| Hessian Calls |
12 |
Active Constraints |
3 |
| Objective Function |
-47.76109086 |
Max Abs Gradient Element |
1.8637499E-6 |
| Lambda |
0 |
Actual Over Pred Change |
0 |
| Radius |
0.0024776027 |
|
|
| GCONV convergence criterion satisfied. |
|
The output lists the optimal parameters with the gradient.
Output 5.8.2: Optimization Results
The three equality constraints are satisfied at the solution.
Output 5.8.3: Linear Constraints at Solution
|
| PROC NLP: Nonlinear Minimization |
| Linear Constraints Evaluated at Solution |
| 1 |
ACT |
-3.608E-16 |
= |
2.0000 |
- |
1.0000 |
* |
x1 |
- |
2.0000 |
* |
x2 |
- |
2.0000 |
* |
x3 |
- |
1.0000 |
* |
x6 |
- |
1.0000 |
* |
x10 |
| 2 |
ACT |
2.2204E-16 |
= |
1.0000 |
- |
1.0000 |
* |
x4 |
- |
2.0000 |
* |
x5 |
- |
1.0000 |
* |
x6 |
- |
1.0000 |
* |
x7 |
|
|
|
|
| 3 |
ACT |
-1.943E-16 |
= |
1.0000 |
- |
1.0000 |
* |
x3 |
- |
1.0000 |
* |
x7 |
- |
1.0000 |
* |
x8 |
- |
2.0000 |
* |
x9 |
- |
1.0000 |
* |
x10 |
|
The Lagrange multipliers and the projected gradient are displayed also.
Output 5.8.4: Lagrange Multipliers
|
| PROC NLP: Nonlinear Minimization |
| First Order Lagrange Multipliers |
| Active Constraint |
Lagrange
Multiplier |
| Linear EC |
[1] |
9.785055 |
| Linear EC |
[2] |
12.968921 |
| Linear EC |
[3] |
15.222060 |
|
The elements of the projected gradient must be small to
satisfy a necessary first-order optimality condition.
Output 5.8.5: Projected Gradient
|
| PROC NLP: Nonlinear Minimization |
| Projected Gradient |
Free
Dimension |
Projected
Gradient |
| 1 |
4.5770108E-9 |
| 2 |
6.868355E-10 |
| 3 |
-7.283013E-9 |
| 4 |
-0.000001864 |
| 5 |
-0.000001434 |
| 6 |
-0.000001361 |
| 7 |
-0.000000294 |
|
The projected Hessian matrix is positive definite satisfying
the second-order optimality condition.
|
| PROC NLP: Nonlinear Minimization |
| Hessian Matrix |
| |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
x10 |
| x1 |
23.978970416 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
| x2 |
-0.610337369 |
6.1587537849 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
| x3 |
-0.610337369 |
-0.610337369 |
0.6665517048 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
| x4 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
706.49329433 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
| x5 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
1.4504700999 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
| x6 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
1442.0329798 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
| x7 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
35.887037191 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
| x8 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
55.108400975 |
-0.610337369 |
-0.610337369 |
| x9 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
26.188980996 |
-0.610337369 |
| x10 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
-0.610337369 |
9.7126336107 |
| Projected Hessian Matrix |
| |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
| X1 |
20.903196985 |
-0.122067474 |
2.6480263467 |
3.3439156526 |
-1.373829641 |
-1.491808185 |
1.1462413516 |
| X2 |
-0.122067474 |
565.97299938 |
106.54631863 |
-83.7084843 |
-37.43971036 |
-36.20703737 |
-16.635529 |
| X3 |
2.6480263467 |
106.54631863 |
1052.3567179 |
-115.230587 |
182.89278895 |
175.97949593 |
-57.04158208 |
| X4 |
3.3439156526 |
-83.7084843 |
-115.230587 |
37.529977667 |
-4.621642366 |
-4.574152161 |
10.306551561 |
| X5 |
-1.373829641 |
-37.43971036 |
182.89278895 |
-4.621642366 |
79.326057844 |
22.960487404 |
-12.69831637 |
| X6 |
-1.491808185 |
-36.20703737 |
175.97949593 |
-4.574152161 |
22.960487404 |
66.669897023 |
-8.121228758 |
| X7 |
1.1462413516 |
-16.635529 |
-57.04158208 |
10.306551561 |
-12.69831637 |
-8.121228758 |
14.690478023 |
|
Output 5.8.6: Projected Hessian Matrix
The following PROC NLP call uses a specified analytical gradient
and the Hessian matrix is computed by finite difference
approximations based on the analytic gradient:
proc nlp tech=tr fdhessian all;
array c[10] -6.089 -17.164 -34.054 -5.914 -24.721
-14.986 -24.100 -10.708 -26.662 -22.179;
array x[10] x1-x10;
array g[10] g1-g10;
min y;
parms x1-x10 = .1;
bounds 1.e-6 <= x1-x10;
lincon 2. = x1 + 2. * x2 + 2. * x3 + x6 + x10,
1. = x4 + 2. * x5 + x6 + x7,
1. = x3 + x7 + x8 + 2. * x9 + x10;
s = x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10;
y = 0.;
do j = 1 to 10;
y = y + x[j] * (c[j] + log(x[j] / s));
g[j] = c[j] + log(x[j] / s);
end;
run;
The results are almost identical to those of the former run.
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
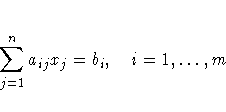
![f(x) = \sum_{j=1}^n x_j [c_j + ln({x_j \over s})]](images/nlpeq213.gif)
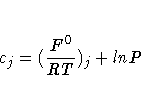
![]() is the model standard free
energy function for the jth compound (that is found
in tables) and P is the total pressure in atmospheres.
is the model standard free
energy function for the jth compound (that is found
in tables) and P is the total pressure in atmospheres.
![]() at temperature
T= 3500oK and pressure P= 750 psi.
at temperature
T= 3500oK and pressure P= 750 psi.