Example 5.1: Using the DATA= Option

The NLP Procedure

Example 5.1: Using the DATA= Option

This example illustrates the use of the DATA= option. The Bard function (refer to More et al. 1981) is a least-squares problem with n=3 parameters and m=15 functions f_k:

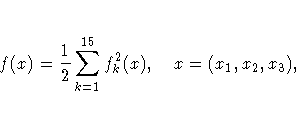
$f(x) = {1 \over 2} \sum_{k=1}^{15} f_k^2(x) , x = (x_1,x_2,x_3) ,$

where

minf_k(x) = y_k - ( x₁ + [(u_k)/(v_k x₂ + w_k x₃)] )

with u_k=k, v_k=16-k, w_k = min(u_k, v_k), and

y_k= .14, .18, .22, .25, .29, .32, .35, .39, .37, .58, .73, .96, 1.34, 2.10, 4.39

The minimum function value f(x^*) = 4.107e-3 is at the point (0.08,1.13,2.34). The starting point x⁰ = (1,1,1) is used.

The following is the naive way of specifying the objective function.

proc nlp tech=levmar;
   lsq y1-y15;
   parms x1-x3 = 1;
   tmp1 = 15 * x2 + min(1,15) * x3;
   y1 = 0.14 - (x1 + 1 / tmp1);
   tmp1 = 14 * x2 + min(2,14) * x3;
   y2 = 0.18 - (x1 + 2 / tmp1);
   tmp1 = 13 * x2 + min(3,13) * x3;
   y3 = 0.22 - (x1 + 3 / tmp1);
   tmp1 = 12 * x2 + min(4,12) * x3;
   y4 = 0.25 - (x1 + 4 / tmp1);
   tmp1 = 11 * x2 + min(5,11) * x3;
   y5 = 0.29 - (x1 + 5 / tmp1);
   tmp1 = 10 * x2 + min(6,10) * x3;
   y6 = 0.32 - (x1 + 6 / tmp1);
   tmp1 = 9 * x2 + min(7,9) * x3;
   y7 = 0.35 - (x1 + 7 / tmp1);
   tmp1 = 8 * x2 + min(8,8) * x3;
   y8 = 0.39 - (x1 + 8 / tmp1);
   tmp1 = 7 * x2 + min(9,7) * x3;
   y9 = 0.37 - (x1 + 9 / tmp1);
   tmp1 = 6 * x2 + min(10,6) * x3;
   y10 = 0.58 - (x1 + 10 / tmp1);
   tmp1 = 5 * x2 + min(11,5) * x3;
   y11 = 0.73 - (x1 + 11 / tmp1);
   tmp1 = 4 * x2 + min(12,4) * x3;
   y12 = 0.96 - (x1 + 12 / tmp1);
   tmp1 = 3 * x2 + min(13,3) * x3;
   y13 = 1.34 - (x1 + 13 / tmp1);
   tmp1 = 2 * x2 + min(14,2) * x3;
   y14 = 2.10 - (x1 + 14 / tmp1);
   tmp1 = 1 * x2 + min(15,1) * x3;
   y15 = 4.39 - (x1 + 15 / tmp1);
run;

A more economical way to program this problem uses the DATA= option to input the 16 terms in f(x).

data bard;
 input r @@;
   w1 = 16. - _n_;
   w2 = min(_n_ , 16. - _n_);
 datalines;
   .14  .18  .22  .25  .29  .32  .35  .39
   .37  .58  .73  .96 1.34 2.10 4.39
  ;
proc nlp data=bard tech=levmar;
   lsq y;
   parms x1-x3 = 1.;
   y = r - (x1 + _obs_ / (w1 * x2 + w2 * x3));
end;

Another way you can specify the objective function uses the ARRAY statement and an explicit do loop, as in the following code.

proc nlp tech=levmar;15] .14  .18  .22  .25  .29  .32  .35  .39  .37  .58
               .73  .96 1.34 2.10 4.39 ;15] y1-y15;
   lsq y1-y15;
   parms x1-x3 = 1.;
   do i = 1 to 15;
     w1 = 16. - i;
     w2 = min(i , w1);
     w3 = w1 * x2 + w2 *i] = (x1 + i];
   end;
run;

Chapter Contents
Previous
Next
Top