Goodness of Fit
The log-likelihood can be expressed in terms of the
mean parameter 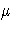 and the log-likelihood-ratio
statistic is the scaled deviance
and the log-likelihood-ratio
statistic is the scaled deviance

where  is the log-likelihood under the model
and
is the log-likelihood under the model
and  is
the log-likelihood under the maximum achievable (saturated) model.
is
the log-likelihood under the maximum achievable (saturated) model.
For generalized linear models,
the scaled deviance can be expressed as

where 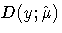 is the residual deviance
for the model and is the sum of individual deviance contributions.
is the residual deviance
for the model and is the sum of individual deviance contributions.
The forms of the individual deviance contributions,
di, are
- Normal

- Inverse Gaussian

- Gamma

- Poisson

- Binomial

where y=r/m, r is the number of successes in m trials.
For a binomial distribution with mi
trials in the ith observation, the Pearson
 statistic is
statistic is

For other distributions, the Pearson
 statistic is
statistic is

The scaled Pearson  statistic is
statistic is  /
/  .Either the mean deviance
.Either the mean deviance 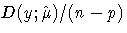 or
the mean Pearson
or
the mean Pearson  statistic
statistic  can be used to estimate the dispersion parameter
can be used to estimate the dispersion parameter  .The
.The  approximation is usually quite accurate for
the differences of deviances for nested models (McCullagh and Nelder 1989).
approximation is usually quite accurate for
the differences of deviances for nested models (McCullagh and Nelder 1989).
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.



