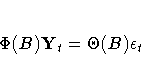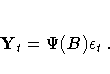RATIO Function

Language Reference

RATIO Function

divides matrix polynomials

returns a matrix containing the terms of $\Phi (B)^{-1} \Theta (B)$ considered as a matrix of rational functions in B that have been expanded as power series

RATIO( ar, ma, terms<, dim>)

The inputs to the RATIO function are as follows:

ar: is an n ×(ns) matrix representing a matrix polynomial generating function, $\Phi (B)$ , in the variable B. The first n ×n submatrix represents the constant term and must be nonsingular, the second n ×n submatrix represents the first order coefficients, and so on.
ma: is an n ×(mt) matrix representing a matrix polynomial generating function, $\Theta (B)$ , in the variable B. The first n ×m submatrix represents the constant term, the second n ×m submatrix represents the first order term, and so on.
terms: is a scalar containing the number of terms to be computed, denoted by r in the discussion below. This value must be positive.
dim: is a scalar containing the value of m above. The default value is 1.

The RATIO function multiplies a matrix of polynomials by the inverse of another matrix of polynomials. It is useful for expressing univariate and multivariate ARMA models in pure moving-average or pure autoregressive forms.

Note that the order of the first two arguments is reversed from the corresponding PROC MATRIX function.

The value returned is an n ×(mr) matrix containing the terms of $\Phi (B)^{-1} \Theta (B)$ considered as a matrix of rational functions in B that have been expanded as power series.

Note: The RATIO function can be used to consolidate the matrix operators employed in a multivariate time-series model of the form

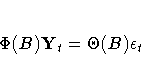
$\Phi (B) Y_t = \Theta (B) \epsilon_t$

where $\Phi (B)$ and $\Theta (B)$ are matrix polynomial operators whose first matrix coefficients are identity matrices. The RATIO function can be used to compute a truncated form of $\Psi (B) = \Phi (B)^{-1} \Theta (B)$ for the equivalent infinite order model

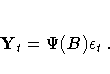
$Y_t = \Psi (B) \epsilon_t .$

The RATIO function can also be employed for simple scalar polynomial division, giving a truncated form of $\theta (x)/\phi (x)$ for two scalar polynomials $\theta (x)$ and $\phi (x)$ .

The cumulative sum of the elements of a column vector x can be obtained using

    ratio({ 1 -1} ,x,ncol(x));

Consider the following example for multivariate ARMA(1,1):

      ar={1 0 -.5  2,
          0 1   3 -.8};
      ma={1 0 .9  .7,
          0 1   2 -.4};
      psi=ratio(ar,ma,4,2);

The matrix produced in

           PSI
             1    0   1.4  -1.3   2.7  -1.45  11.35
   :    -9.165

             0    1    -1   0.4   -5   4.22  -12.1
   :     7.726

Chapter Contents
Previous
Next
Top