General Notation for ARIMA Models

The ARIMA Procedure

General Notation for ARIMA Models

ARIMA is an acronym for AutoRegressive Integrated Moving-Average. The order of an ARIMA model is usually denoted by the notation ARIMA(p,d,q), where

p: is the order of the autoregressive part
d: is the order of the differencing
q: is the order of the moving-average process

If no differencing is done (d = 0), the models are usually referred to as ARMA(p,q) models. The final model in the preceding example is an ARIMA(1,1,1) model since the IDENTIFY statement specified d = 1, and the final ESTIMATE statement specified p = 1 and q = 1.

Notation for Pure ARIMA Models

Mathematically the pure ARIMA model is written as

$W_{t}={\mu}+\frac{{\theta}(B)}{{\phi}(B)}a_{t}$

where

t: indexes time
W_t: is the response series Y_t or a difference of the response series
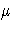
${\mu}$: is the mean term
B: is the backshift operator; that is, BX_t=X_t-1
${{\phi}(B)}$: is the autoregressive operator, represented as a polynomial in the back shift operator: ${{\phi}(B)=1-{\phi}_{1}B-{ ... }-{\phi}_{p}B^p}$
${{\theta}(B)}$: is the moving-average operator, represented as a polynomial in the back shift operator: ${{\theta}(B)=1-{\theta}_{1}B-{ ... }-{\theta}_{q}B^q}$
a_t: is the independent disturbance, also called the random error.

The series W_t is computed by the IDENTIFY statement and is the series processed by the ESTIMATE statement. Thus, W_t is either the response series Y_t or a difference of Y_t specified by the differencing operators in the IDENTIFY statement.

For simple (nonseasonal) differencing, W_t=(1-B)^dY_t . For seasonal differencing W_t=(1-B)^d(1-B^s)^DY_t, where d is the degree of nonseasonal differencing, D is the degree of seasonal differencing, and s is the length of the seasonal cycle.

For example, the mathematical form of the ARIMA(1,1,1) model estimated in the preceding example is

$(1-B)Y_{t}={\mu}+\frac{(1-{\theta}_{1}B)}{(1-{\phi}_{1}B)}a_{t}$

Model Constant Term

The ARIMA model can also be written as

${\phi}(B)(W_{t}-{\mu})={\theta}(B)a_{t}$

${\phi}(B)W_{t}=const+{\theta}(B)a_{t}$

where

$const = {\phi}(B){\mu} = {\mu}-{\phi}_{1}{\mu}-{\phi}_{2}{\mu}-{ ... }-{\phi}_{p}{\mu}$

Thus, when an autoregressive operator and a mean term are both included in the model, the constant term for the model can be represented as ${{\phi}(B){\mu}}$ . This value is printed with the label "Constant Estimate" in the ESTIMATE statement output.

Notation for Transfer Function Models

The general ARIMA model with input series, also called the ARIMAX model, is written as

$W_{t}={\mu} +\sum_{i}^{}{\frac{{\omega}_{i}(B)}{{\delta}_{i}(B) }B^{k_{i}}X_{i,t}} +\frac{{\theta}(B)}{{\phi}(B)}a_{t}$

where

X_i,t: is the ith input time series or a difference of the ith input series at time t
k_i: is the pure time delay for the effect of the ith input series
${{\omega}_{i}(B)}$: is the numerator polynomial of the transfer function for the ith input series
${{\delta}_{i}(B)}$: is the denominator polynomial of the transfer function for the ith input series.

The model can also be written more compactly as

$W_{t}={\mu}+\sum_{i}^{}{{\Psi}_{i}(B)X_{i,t}}+n_{t}$

where

${{\Psi}_{i}(B)}$: is the transfer function weights for the ith input series modeled as a ratio of the ${\omega}$ and ${\delta}$ polynomials: ${{\Psi}_{i}(B)=({\omega}_{i}(B)/{\delta}_{i}(B))B^{k_{i}}}$
n_t: is the noise series: ${n_{t}=({\theta}(B)/{\phi}(B))a_{t}}$

This model expresses the response series as a combination of past values of the random shocks and past values of other input series. The response series is also called the dependent series or output series. An input time series is also referred to as an independent series or a predictor series. Response variable, dependent variable, independent variable, or predictor variable are other terms often used.

Notation for Factored Models

ARIMA models are sometimes expressed in a factored form. This means that the 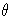${\phi}$ , ${\theta}$ , ${\omega}$ , or ${\delta}$ polynomials are expressed as products of simpler polynomials. For example, we could express the pure ARIMA model as

$W_{t}={\mu} +\frac{{\theta}_{1}(B){\theta}_{2}(B)}{{\phi}_{1}(B){\phi}_{2}(B)}a_{t}$

where ${{\phi}_{1}(B){\phi}_{2}(B)={\phi}(B)}$ and ${{\theta}_{1}(B){\theta}_{2}(B)={\theta}(B)}$ .

When an ARIMA model is expressed in factored form, the order of the model is usually expressed using a factored notation also. The order of an ARIMA model expressed as the product of two factors is denoted as ARIMA(p,d,q)×(P,D,Q).

Notation for Seasonal Models

ARIMA models for time series with regular seasonal fluctuations often use differencing operators and autoregressive and moving average parameters at lags that are multiples of the length of the seasonal cycle. When all the terms in an ARIMA model factor refer to lags that are a multiple of a constant s, the constant is factored out and suffixed to the ARIMA(p,d,q) notation.

Thus, the general notation for the order of a seasonal ARIMA model with both seasonal and nonseasonal factors is ARIMA(p,d,q)×(P,D,Q)_s. The term (p,d,q) gives the order of the nonseasonal part of the ARIMA model; the term (P,D,Q)_s gives the order of the seasonal part. The value of s is the number of observations in a seasonal cycle: 12 for monthly series, 4 for quarterly series, 7 for daily series with day-of-week effects, and so forth.

For example, the notation ARIMA(0,1,2)×(0,1,1)₁₂ describes a seasonal ARIMA model for monthly data with the following mathematical form:

$(1-B)(1-B^{12})Y_{t}={\mu} +(1-{\theta}_{1,1}B-{\theta}_{1,2}B^2) (1-{\theta}_{2,1}B^{12})a_{t}$

Chapter Contents
Previous
Next
Top