The One-Way Random Effects Model

The TSCSREG Procedure

The One-Way Random Effects Model

The specification for the one-way random effects model is

$u_{it}={\nu}_{i}+{\epsilon}_{it}$

Let Z₀ = diag(j_{T_i}), ${P_{0}=diag({\bar{J}}_{T_{i}})}$ , and Q₀ = diag(E_{T_i}), with ${{\bar{J}}_{T_{i}}=J_{T_{i}}/T_{i}}$ and ${E_{T_{i}}=I_{T_{i}}-{\bar J}_{T_{i}}}$ . Define ${\tilde{X}_{s}=Q_{0}X_{s}}$ and ${\tilde{y}=Q_{0}y}$ .

The fixed effects estimator of ${ {\sigma}^2_{{\epsilon} } }$ is still unbiased under the random effects assumptions, so you need to calculate only the estimate of ${{\sigma}_{{\nu}} }$ .

In the balanced data case, the estimation method for the variance components is the fitting constants method as applied to the one way model; refer to Baltagi and Chang (1994). Fuller and Battese (1974) apply this method to the two-way model.

Let

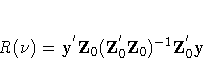
$R({\nu})=y^{'}Z_{0}( Z^{'}_{0}Z_{0})^{-1} Z^{'}_{0}y$

$R({\beta}|{\nu})=(( \tilde{X}^{'}_{s} \tilde{X}_{s})^{-1} \tilde{X}^{'}_{s}\tilde{y} )^{'} ( \tilde{X}^{'}_{s}\tilde{y})$

$R({\beta})=(X^{'}y)^{'} (X^{'}X) ^{-1}X^{'}y$

$R({\nu}|{\beta})=R({\beta}|{\nu})+R({\nu})-R({\beta})$

The estimator of the error variance is given by

$\hat{{\sigma}}_{{\epsilon}}^2= (y^{'}y - R({\beta}|{\nu}) - R({\nu}) ) / (M-N-(K-1))$

and the estimator of the cross-sectional variance component is given by

$\hat{{\sigma}}_{{\nu}}^2= (R({\nu}|{\beta}) - (N-1)\hat{{\sigma}}_{{\epsilon}}^2 ) /(M - \rm{tr}( Z^{'}_{0}X (X^{'}X)^{-1}X^{'}Z_{0} ))$

The estimation of the one-way unbalanced data model is performed using a specialization (Baltagi and Chang 1994) of the approach used by Wansbeek and Kapteyn (1989) for unbalanced two-way models.

The estimation of the variance components is performed by using a quadratic unbiased estimation (QUE) method. This involves focusing on quadratic forms of the centered residuals, equating their expected values to the realized quadratic forms, and solving for the variance components.

Let

$q_{1}=\tilde{u}^{'}Q_{0}\tilde{u}$

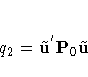
$q_{2}=\tilde{u}^{'}P_{0}\tilde{u}$

where the residuals ${\tilde{u}}$ are given by ${\tilde{u} = (I_{M}-j_{M} j{'}_{M}/M) (y-X_{s} \tilde{X}{'}_{s} \tilde{X}_{s})^{-1} \tilde{X}_{s}{'}\tilde{y} )}$ if there is an intercept and by ${tilde{u}}= (y-X_{s} ( \tilde{X}{'}_{s} \tilde{X}_{s})^{-1} \tilde{X}{'}_{s}\tilde{y} )$ if there is not.

Consider the expected values

$E(q_{1})=(M-N-(K-1)) {\sigma}^2_{{\epsilon}}$

$E(q_{2})=(N-1+ \rm{tr}[( X^{'}_{s}Q_{0}X_{s})^{-1} X^{'}_{s}P_{0}X_{s}]- \rm... ...{s}Q_{0}X_{s})^{-1} X^{'}_{s} {\bar{J}}_{M}X_{s}] ) {\sigma}^2_{{\epsilon}}$

$+[M-(\sum_{i} T^2_{i}/M)] {\sigma}^2_{{\nu}}$

${ \hat{{\sigma}}^2_{{\epsilon}} }$ and ${ \hat{{\sigma}}^2_{{\nu}} }$ are obtained by equating the quadratic forms to their expected values.

The estimated generalized least squares procedure substitutes the QUE estimates into the covariance matrix of u_it, which is given by

$V= {\sigma}^2_{{\nu}} I_{M} + {\sigma}^2_{{\epsilon}} Z_{0} Z^{'}_{0}$

Chapter Contents
Previous
Next
Top