SOLVE Statement

The MODEL Procedure

SOLVE Statement

SOLVE [variables] [SATISFY= equations] [INITIAL= (variable=[parameter]] [/options];

The SOLVE statement specifies that the model be simulated or forecast for input data values and, optionally, selects the variables to be solved. If the list of variables is omitted, all of the model variables declared ENDOGENOUS are solved. If no model variables are declared ENDOGENOUS, then all model variables are solved.

The following specification can be used in the SOLVE statement:

SATISFY= equation
SATISFY= ( equations ): specifies a subset of the model equations that the solution values are to satisfy. If the SATISFY= option is not used, the solution is computed to satisfy all the model equations. Note that the number of equations must equal the number of variables solved.

Data Set Options

DATA= SAS-data-set: names the input data set. The model is solved for each observation read from the DATA= data set. If the DATA= option is not specified on the SOLVE statement, the data set specified by the DATA= option on the PROC MODEL statement is used.
ESTDATA= SAS-data-set: names a data set whose first observation provides values for some or all of the parameters and whose additional observations (if any) give the covariance matrix of the parameter estimates. The covariance matrix read from the ESTDATA= data set is used to generate multivariate normal pseudo-random shocks to the model parameters when the RANDOM= option requests Monte Carlo simulation.
OUT= SAS-data-set: outputs the predicted (solution) values, residual values, actual values, or equation errors from the solution to a data set. Only the solution values are output by default.
OUTACTUAL: outputs the actual values of the solved variables read from the input data set to the OUT= data set. This option is applicable only if the OUT= option is specified.
OUTALL: specifies the OUTACTUAL, OUTERRORS, OUTLAGS, OUTPREDICT, and OUTRESID options
OUTERRORS: writes the equation errors to the OUT= data set. These values are normally very close to zero when a simultaneous solution is computed; they can be used to double-check the accuracy of the solution process. It is applicable only if the OUT= option is specified.
OUTLAGS: writes the observations used to start the lags to the OUT= data set. This option is applicable only if the OUT= option is specified.
OUTPREDICT: writes the solution values to the OUT= data set. This option is relevant only if the OUT= option is specified. The OUTPREDICT option is the default unless one of the other output options is used.
OUTRESID: writes the residual values computed as the difference of the solution values and the values for the solution variables read from the input data set to the OUT= data set. This option is applicable only if the OUT= option is specified.
PARMSDATA= SAS-data-set: specifies a data set that contains the parameter estimates. See the "Input Data Sets" section for more details.
SDATA= SAS-data-set: specifies a data set that provides the covariance matrix of the equation errors. The covariance matrix read from the SDATA= data set is used to generate multivariate normal pseudo-random shocks to the equations when the RANDOM= option requests Monte Carlo simulation.
TYPE= name: specifies the estimation type. The name specified in the TYPE= option is compared to the _TYPE_ variable in the ESTDATA= and SDATA= data sets to select observations to use in constructing the covariance matrices. When TYPE= is omitted, the last estimation type in the data set is used.

Solution Mode Options: Lag Processing

DYNAMIC: specifies a dynamic solution. In the dynamic solution mode, solved values are used by the lagging functions. DYNAMIC is the default.
NAHEAD= n: specifies a simulation of n-period-ahead dynamic forecasting. The NAHEAD= option is used to simulate the process of using the model to produce successive forecasts to a fixed forecast horizon, with each forecast using the historical data available at the time the forecast is made.

Note that NAHEAD=1 produces a static (one-step-ahead) solution. NAHEAD=2 produces a solution using one-step-ahead solutions for the first lag (LAG1 functions return static predicted values) and actual values for longer lags. NAHEAD=3 produces a solution using NAHEAD=2 solutions for the first lags, NAHEAD=1 solutions for the second lags, and actual values for longer lags. In general, NAHEAD=n solutions use NAHEAD=n-1 solutions for LAG1, NAHEAD=n-2 solutions for LAG2, and so forth.
START= s: specifies static solutions until the sth observation and then changes to dynamic solutions. If the START=s option is specified, the first observation in the range in which LAGn delivers solved predicted values is s+n, while LAGn returns actual values for earlier observations.
STATIC: specifies a static solution. In static solution mode, actual values of the solved variables from the input data set are used by the lagging functions.

Solution Mode Options: Use of Available Data

FORECAST: specifies that the actual value of a solved variable is used as the solution value (instead of the predicted value from the model equations) whenever nonmissing data are available in the input data set. That is, in FORECAST mode, PROC MODEL solves only for those variables that are missing in the input data set.
SIMULATE: specifies that PROC MODEL always solves for all solution variables as a function of the input values of the other variables, even when actual data for some of the solution variables are available in the input data set. SIMULATE is the default.

Solution Mode Options: Numerical Solution Method

JACOBI: computes a simultaneous solution using a Jacobi iteration.
NEWTON: computes a simultaneous solution using Newton's method. When the NEWTON option is selected, the analytic derivatives of the equation errors with respect to the solution variables are computed and memory-efficient sparse matrix techniques are used for factoring the Jacobian matrix.

The NEWTON option can be used to solve both normalized-form and general-form equations and can compute goal-seeking solutions. NEWTON is the default.
SEIDEL: computes a simultaneous solution using a Gauss-Seidel method.
SINGLE
ONEPASS: specifies a single-equation (nonsimultaneous) solution. The model is executed once to compute predicted values for the variables from the actual values of the other endogenous variables. The SINGLE option can only be used for normalized-form equations and cannot be used for goal-seeking solutions.

For more information on these options, see the "Solution Modes" section later in this chapter.

Monte Carlo Simulation Options

QUASI= NONE|SOBOL|FAURE: specifies a psuedo or quasi-random number generator. Two Quasi-random number generators supported by the MODEL procedure, the Sobol sequence (QUASI=SOBOL) and the Faure sequence (QUASI=FAURE). The default is QUASI=NONE which is the psuedo random number generator.
RANDOM= n: repeats the solution n times for each BY group, with different random perturbations of the equation errors if the SDATA= option is used; with different random perturbations of the parameters if the ESTDATA= option is used and the ESTDATA= data set contains a parameter covariance matrix; and with different values returned from the random-number generator functions, if any are used in the model program. If RANDOM=0, the random-number generator functions always return zero. See "Monte Carlo Simulation" for details. The default is RANDOM=0.
SEED= n: specifies an integer to use as the seed in generating pseudo-random numbers to shock the parameters and equations when the ESTDATA= or the SDATA= options are specified. If n is negative or zero, the time of day from the computer's clock is used as the seed. The SEED= option is only relevant if the RANDOM= option is used. The default is SEED=0.

Options for Controlling the Numerical Solution Process

The following options are useful when you have difficulty converging to the simultaneous solution.

CONVERGE= value

specifies the convergence criterion for the simultaneous solution. Convergence of the solution is judged by comparing the CONVERGE= value to the maximum over the equations of

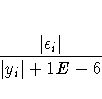
$\frac{|{\epsilon}_{i}|}{| y_{i}|+1E-6}$

if it is computable, otherwise

$|{\epsilon}_{i}|$

where ${\epsilon}$ _i represents the equation error and y_i represents the solution variable corresponding to the ith equation for normalized-form equations. The default is CONVERGE=1E-8.

MAXITER= n

specifies the maximum number of iterations allowed for computing the simultaneous solution for any observation. The default is MAXITER=50.

INITIAL= (variable= [parameter])

specifies starting values for the parameters

MAXSUBITER= n

specifies the maximum number of damping subiterations that are performed in solving a nonlinear system when using the NEWTON solution method. Damping is disabled by setting MAXSUBITER=0. The default is MAXSUBITER=10.

Printing Options

INTGPRINT: prints between data points integration values for the DERT. variables and the auxiliary variables. If you specify the DETAILS option, the integrated derivative variables are printed as well.
ITPRINT: prints the solution approximation and equation errors at each iteration for each observation. This option can produce voluminous output.
PRINTALL: specifies the printing control options DETAILS, ITPRINT, SOLVEPRINT, STATS, and THEIL.
SOLVEPRINT: prints the solution values and residuals at each observation
STATS: prints various summary statistics for the solution values
THEIL: prints tables of Theil inequality coefficients and Theil relative change forecast error measures for the solution values. See "Summary Statistics" in the "Details" section for more information.

Other Options

Other options that can be used on the SOLVE statement include the following that list and analyze the model: BLOCK, GRAPH, LIST, LISTCODE, LISTDEP, LISTDER, and XREF. The LTEBOUND= and MINTIMESTEP= options can be used to control the integration process. The following printing-control options are also available: DETAILS, FLOW, MAXERRORS=, NOPRINT, and TRACE. For complete descriptions of these options, see the PROC MODEL and FIT statement options described earlier in this chapter.

Chapter Contents
Previous
Next
Top