Dealing with Vectors

Vector Components
Any vector can be expressed as a sum of a number of other vectors. The vectors which are summed are called the components of the original vector. When you want to add and subtract two dimensional vectors, it is convenient to express a vector as a sum of two components which are at right angles to each other. Typically one component is along a horizontal axis, and another vector is vertical. Any two dimensional vector can be expressed as a sum of one horizontal component and one vertical component. (In three dimensions it is necessary to add a third component at right angles to the other two.)

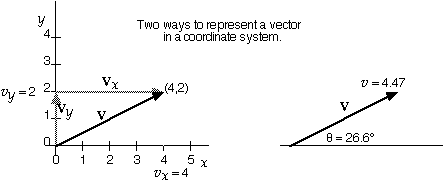
In the figure the vector v is a sum of vectors v_x and v_y:

v = v_x + v_y

The length of v_x is written as v_x without the bold face v. Likewise, the length of v_y is written as v_y.
You get the length of the the vector by adding the lengths of the components using the rule of Pythogoras:

v² = v_x² + v_y²

The vector in our diagram has v_x = 4 and v_y =2 so v = 4.47.
One can convey the direction of the vector by stating the angle it makes with the x axis, taking positive angles to be counterclockwise. From trigonometry the angle is

$$ \theta = \tan^{-1}\left(\frac{v_y}{v_x}\right) $$

Here tan^-1 means inverse tangent or arctangent not 1/tangent. (Computer applications often use "ATAN(x)" for the arctangent function.) In the example in the figure, tan^-1(2/4) = 26.6 degrees.
If you know the length and angle (θ) of a vector you can get the size of the components from trigonometry as follows:

v_x = v cos θ
v_y = v sin θ

Try calculating the components from the length and angle of our example, 4.47 and 26.6 deg. There will be some round-off error but the answer should be accurate to three significant figures.
The rule for defining an angle may not be understood by your reader, so it is always a good idea to say how you do it. (For example, sometimes the angle may be referred to the y axis with positive angles being clockwise. In which case the angle of our vector would be 63.4 deg.) Furthermore, all of the ways of expressing vectors in terms of scalar numbers (x and y components or length and angle depend on the choice of coordinate system. The x axis does not have to be horizontal and the y axis is not required to be vertical. If you choose another coordinate system then the numbers you get change, even though the vector remains the same. So when you refer to vectors by scalar components you have to give the coordinate system too.

Dealing with vectors in three dimensions is more complicated. In the component representation, there are three components. If you express the vector using length and angle, there is still one length but there are two angles to specify, not one.

Adding and subtracting vectors
When you have a problem involving vectors, it's important to realize that vectors are not numbers. In particular you MUST add and subtract them like vectors. Do not plug numbers into a vector equation or formula. We have shown you a simple geometrical representation of adding and subtracting vectors and you can do vector calculations by drawing an accurate scale diagram. Add and subtract by using the rules we gave for the arrow representation of vectors. (This works best in two dimensions.)
I recommend considering three ways to do vector calculations. Choose the one which seems best for you and your problem.

Three ways to calculate with vectors

Draw an accurate scale drawing. You can multiply by scalars, add and subtract graphically, taking care to be as exact as possible. Measure the magnitudes and directions of the resulting vectors.

Use trigonometry. Some rules of trigonometry, such as the law of Pythogoras, apply only for right triangles. However, there are other, more complicated rules for general triangles such as the cosine law.

Establish a rectangular coordinate system and find the components of all vectors with respect to that coordinate system. Multiply by scalars, add and subtract the magnitudes of the components using algebra.

Example: Airplane travelling in the wind
Here is an example of an airplane travelling in the wind. The airplane flies in the air 100 km/h 30 degrees north of due east. However the wind is blowing at 45°south of due west (SW) at 20 km/h. What is the velocity, speed and direction, that the plane travels with respect to the ground?

We can construct a scale drawing of the velocity vectors. Add the velocity of the plane with respect to the air, v_pa to the velocity of the air with respect to the ground, v_ag. The sum is the velocity of the plane with respect to the ground, v_pg:

v_pg = v_pa + v_ag

This is a vector equation. The sum of the speeds, 100 km/h + 20 km/h, is not the resultant speed. You can measure the scale drawing to get a fair idea of the result. We can also do the problem by vector components:

Find x components and add them:

v_pax = v_pa cos(θ_pa) = 100 km/h cos(30°) = 86.6 km/h
v_agx = v_ag cos(θ_ag) = 20 km/h cos(225°) = −14.1 km/h

v_pgx = 86.6 km/h − 14.1 km/h = 72.5 km/h

Find the y components and add them

v_pay = v_pa sin(θ_pa) = 100 km/h sin(30°) = 50 km/h
v_agy = v_ag sin(θ_ag) = 20 km/h sin(225°) = −14.1 km/h

v_pgy = 50 km/h − 14.1 km/h = 35.9 km/h

Find magnitude and direction of resultant:

$v_{\rm pg} = \sqrt{v^2_{\rm pgx} + v^2_{\rm pgy}}$ = 80.8 km/h

$\theta = \arctan{\left(\frac{v_{\rm pgy}}{v_{\rm pgx}}\right)}$ = 26.3°