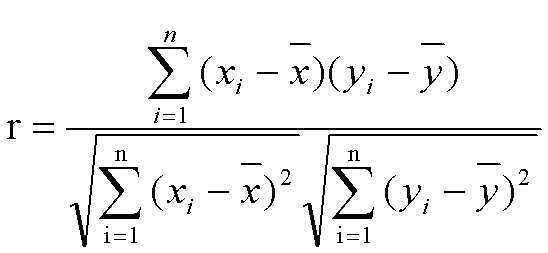
Analysis: Comparing the Deprivation Scores
Correlation
We included a correlation test as well to exhibit the comparison strength of the deprivation scores. Correlation is a statistical method to study the joint behavior of two variables to test for their level of significance. Correlation tests were run at the DA, CT and LHA level in GVRD. We also ran a comparison within New Westminster at the CT and DA level. All values entered into the correlation were scaled between 0 and 1. Zero represented the least deprivation and 1 represented the most deprivation. A scatter matrix plot was created in S-Plus for visual comparison between all indices.
Correlation was calculated as:
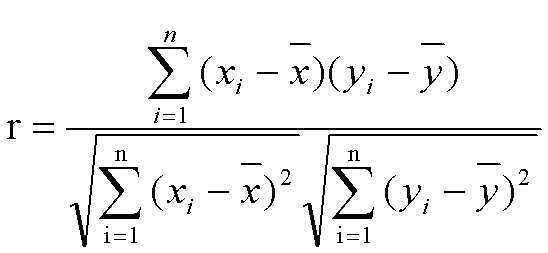
Correlation tests fell between -1 and 1; while 1 and -1 represented the perfect relationship between the variables. Positive numbers represent a positive relationship and negative numbers represent a reverse relationship. Correlation coefficients equals to zero represent no relationship between the two variables.
Testing for the Absence of Correlation
In addition, a hypothesis test determines whether the absence of correlation exists between two variables. The absence of correlation test assumed the data were drawn from a bivariate normal distribution in which both and are normally distributed. A hypothesis test is valid when the sample size is larger than 30, which will exclude the values of the GVRD at LHA and New Westminster at CT level. Hypothesis Ho : p = 0 as there was no correlation between the two scores. For the Alternative Hypothesis, we looked at Ha: p >0 as we wanted to identify positive relationships between the indices. If the null hypothesis was rejected there was a relationship between the two indices.
Spatial Autocorrelation of the Indices
Spatial autocorrelation was executed at all three levels of our analysis. The calculation for spatial autocorrelation was run using the MapStat extension in the ESRI software platform ArcView 3.3. We chose to run a calculation for autocorrelation using the Moran's I technique. Before the calculation was run, deprivation scores were queried based on the mean score of the index. All values that were greater than one deviation from the mean were assigned a value of 1 and all values less then one standard deviation were assigned a value of zero. This reason for separating the deprivation scores based on their standard deviation was subjective. The purpose of this phase was simply to identify those units that were significantly above the mean value by one standard deviation.
Result
Correlation
GVRD Correlation (LHA)
|
Jarman
|
SCOTDEP
|
SDD
|
Townsend
|
|
| DETR |
0.507
|
0.535
|
0.406
|
0.645
|
| Jarman |
-
|
0.957
|
0.106
|
0.785
|
| SCOTDEP |
-
|
-
|
0.127
|
0.689
|
| SDD |
-
|
-
|
-
|
0.260
|
GVRD Correlation (CT)
|
Jarman
|
SCOTDEP
|
SDD
|
Townsend
|
|
| DETR |
0.415
|
0.326
|
0.437
|
0.627
|
| Jarman |
-
|
0.980
|
0.342
|
0.487
|
| SCOTDEP |
-
|
-
|
0.330
|
0.373
|
| SDD |
-
|
-
|
-
|
0.332
|
GVRD Correlation (DA)
|
Jarman
|
SCOTDEP
|
SDD
|
Townsend
|
|
| DETR |
0.461
|
0.525
|
0.531
|
0.585
|
| Jarman |
-
|
0.528
|
0.397
|
0.625
|
| SCOTDEP |
-
|
-
|
0.400
|
0.670
|
| SDD |
-
|
-
|
-
|
0.358
|
New Westminster Correlation (CT)
|
Jarman
|
SCOTDEP
|
SDD
|
Townsend
|
|
| DETR |
0.594
|
0.627
|
0.848
|
0.457
|
| Jarman |
-
|
0.822
|
0.792
|
0.905
|
| SCOTDEP |
-
|
-
|
0.896
|
0.915
|
| SDD |
-
|
-
|
-
|
0.783
|
GVRD Correlation (DA)
|
Jarman
|
SCOTDEP
|
SDD
|
Townsend
|
|
| DETR |
0.534
|
0.715
|
0.761
|
0.715
|
| Jarman |
-
|
0.509
|
0.669
|
0.560
|
| SCOTDEP |
-
|
-
|
0.763
|
0.835
|
| SDD |
-
|
-
|
-
|
0.755
|
All correlation results displayed a positive relationship. In general, the GVRD LHA correlation is higher than the DA and CT levels. When the comparisons involve the SDD index the correlation is reversed. In all cases, the CT units displayed a higher correlation than the DA level except when incorporating the SDD index. If the SDD index is compared to the other indices, it will have a higher correlation at the more detail level than the general level. However, when the other indices are compared to each other they signify a stronger relationship at a smaller scale than at a larger scale. Both the SCOTDEP and Jarman indices demonstrated a very high correlation at the LHA and CT level in GVRD. This was presumable as the SCOTDEP index used four of the original eight Jarman variables to calculate deprivation. The New Westminster CT units generated a higher correlation value than the DA units within all the indices except DETR VS SCOTDEP and DETR VS TOWNSAND. Again, this pattern was not reflected when incorporating the SDD index into the New Westminster calculations. In all of the tests, the aggregation of data into smaller scales exhibited a stronger correlation.
Testing for the Absence of Correlation
GVRD t value for absence of correlation test (CT)
|
Jarman
|
SCOTDEP
|
SDD
|
Townsend
|
|
| DETR |
16.671
|
13.757
|
17.427
|
25.697
|
| Jarman |
-
|
140.183
|
14.276
|
19.295
|
| SCOTDEP |
-
|
-
|
13.901
|
15.265
|
| SDD |
-
|
-
|
-
|
13.950
|
n = 394; t at 95% = 1.649
GVRD t value for absence of correlation test (DA)
|
Jarman
|
SCOTDEP
|
SDD
|
Townsend
|
|
| DETR |
51.969
|
59.066
|
59.809
|
66.743
|
| Jarman |
-
|
59.381
|
45.599
|
72.529
|
| SCOTDEP |
-
|
-
|
45.874
|
80.058
|
| SDD |
-
|
-
|
-
|
41.930
|
n = 3159; t at 95% = 1.645
New Westminster t value for absence of correlation test (DA)
|
Jarman
|
SCOTDEP
|
SDD
|
Townsend
|
|
| DETR |
9.819
|
14.528
|
16.370
|
14.531
|
| Jarman |
-
|
9.325
|
13.044
|
10.333
|
| SCOTDEP |
-
|
-
|
16.462
|
20.596
|
| SDD |
-
|
-
|
-
|
16.110
|
n = 86; t at 95% = 1.663
We rejected all the tests we done. There was correlation between all the indices score in GVRD CT, GVRD DA and New Westminster DA level.
Spatial Autocorrelation
Global Moran Coefficient scores for all deprivation indices at the DA level
| DETR | Jarman | SCOTDEP | SDD | Townsend | |
| MoranCoefficient | 0.200292 | 0.190777 | 0.17759 | 0.233598 | 0.353696 |
| Z-Score | 18.0518 | 17.1956 | 16.009 | 21.0488 | 31.8559 |
Global Moran Coefficient scores for all deprivation indices at the CT level
| DETR | Jarman | SCOTDEP | SDD | Townsend | |
| MoranCoefficient | 0.352506 | 0.0969009 | 0.0862216 | 0.219162 | 0.484241 |
| Z-Score | 10.8705 | 3.03849 | 2.71126 | 6.78471 | 14.9071 |
Global Moran Coefficient scores for all deprivation indices at the LHA level
| DETR | Jarman | SCOTDEP | SDD | Townsend | |
| MoranCoefficient | -0.064916 | <NULL> | <NULL> | -0.041644 | 0.539728 |
| Z-Score | -0.177321 | <NULL> | <NULL> | -0.036008 | 3.49427 |
Within the Jarman and SCOTDEP indices we observed less spatial autocorrelation as scale decreased although no observations above one standard deviation existed for these two indices at the LHA level. In an opposite effect, the Townsend index generated a stronger level of spatial autocorrelation as scale decreased. At the LHA level, however, the spatial autocorrelation may be explained as the three LHA boundaries that we classified as one deviation from the mean were: City Centre, Midtown, and the Downtown Eastside - all of which border each other geographically. As well, the DETR index showed a stronger correlation at the CT level then the DA level, but this then fell to a negative value at the LHA level as only one LHA unit existed after re-scaling. The varied amount of spatial autocorrelation in this analysis is suggestive of the amount of variability within each index.