



The theme of the lectures will be two-fold. Mathematical techniques
will be discussed within the context of simple nonlinear models, the
scope of which will also serve as an introductory survey of nonlinear
PDE phenomena. The simplest methods apply to weakly nonlinear PDEs and
are appropriate for studying multiple end-states (bifurcation theory)
and instabilities. A variety of asymptotic methods for nonlinear
oscillations lead naturally to descriptions for the nonlinear
modulation of waves. Strongly nonlinear spatial structures, like
solitary waves and fronts, give insight into the self-organizing modes
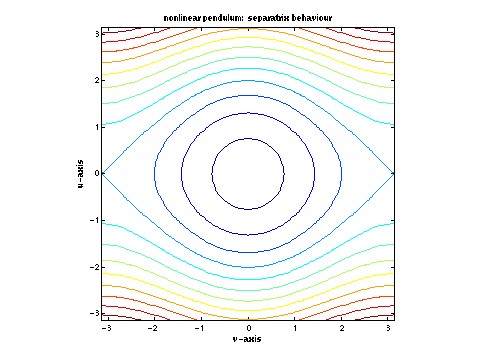
which often arise in the evolution of patterns. Lastly, Hamiltonian
systems offer a bridge between the theories of ODE chaos and PDE
complexity.


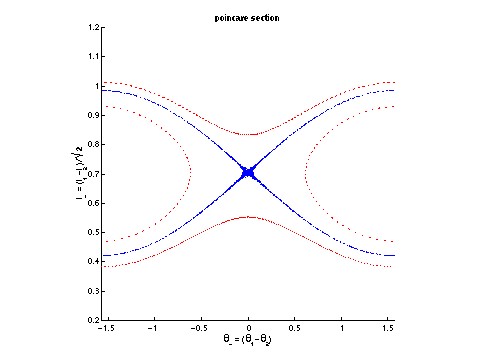
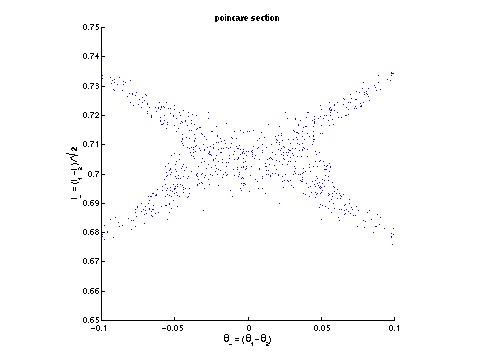
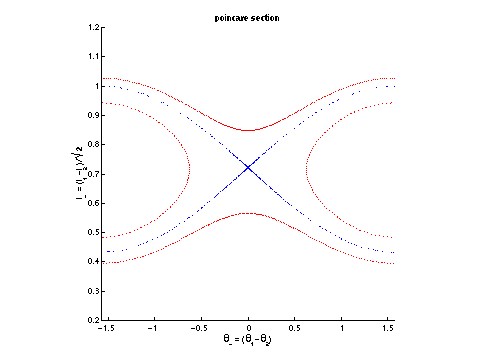
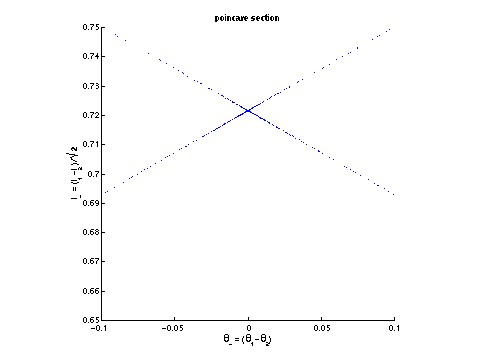
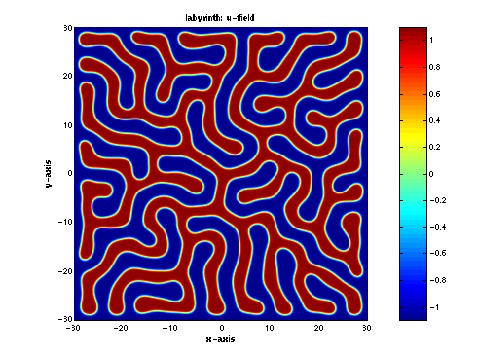
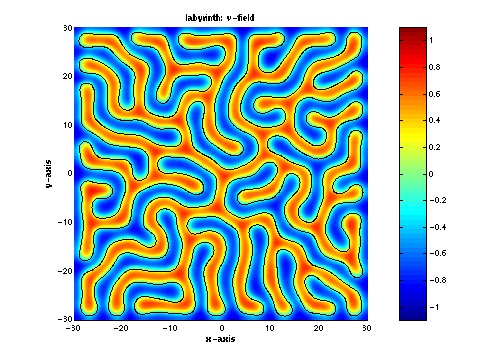
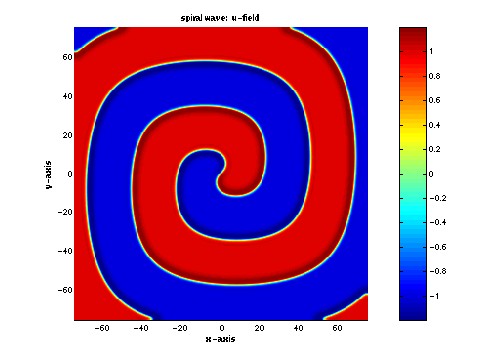
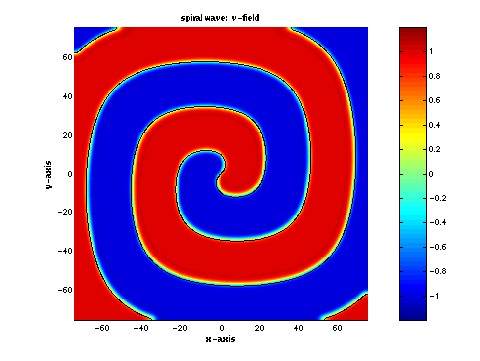



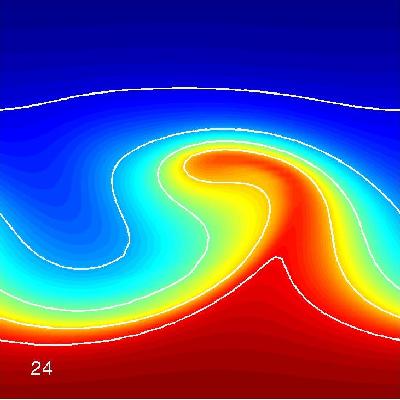
The image on the left is a labyrinthine pattern of
concentration obtained from a model describing a realizable, albeit
slightly esoteric, chemical reaction. The image on the right is a
snapshot of the surface temperature from a model describing the
development of atmospheric storms. In both of these cases,
nonlinearity plays a significant role in determining the formation of
the spatial structure.
