- What is the chance that test detects the condition for this randomly
selected person?
- Assuming that the condition is detected by the test for this randomly
selected person what is the chance that the person has the condition?
- A mandatory testing program is contemplated. If all 200 million are
tested about how many positive results should be expected? Of these
about how many will not have the condition?
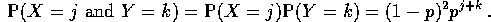
- Let
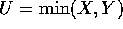 ,
, 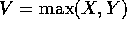 and W=V-U. Express the event
U=j and W=k in terms of X and Y.
and W=V-U. Express the event
U=j and W=k in terms of X and Y.
- Compute
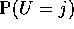 and
and 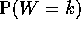 and prove that the event
U=j and the event W=k are independent.
and prove that the event
U=j and the event W=k are independent.
- A computer is waiting for two flags to be set. Both flags start
out not set.
For each flag the conditional probability that the flag is set next cycle
given it is not yet set is 0.5. The two flags operate independently. How
many cycles should you expect to wait before both flags are set including
the cycle on which the last flag becomes set?
SET B
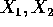 are iid real random variables with
density f . Let
are iid real random variables with
density f . Let 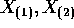 be the X 's arranged
in increasing order, that is, X_(1) is the minimum of
be the X 's arranged
in increasing order, that is, X_(1) is the minimum of 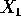 and
and 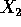 while
while 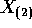 is the maximum.
is the maximum.
- Find the joint density of
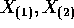 .
.
- Suppose
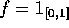 . Prove that
. Prove that 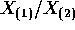 is independent of
is independent of 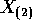 .
.
- Find the density of
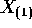 .
.
- Find the density of
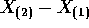 .
.
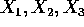 are iid exponential. Let
are iid exponential. Let 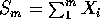 for i=1, 2 and 3.
for i=1, 2 and 3.
- Find the joint density of
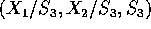 .
.
- Find the joint density of
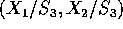 .
.
- Find the joint density of
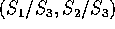 .
.
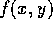 . Prove from the
definition of density that the density of X is
. Prove from the
definition of density that the density of X is 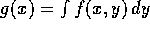 .
.
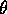 ). After observing X a coin landing
Heads with probability p is tossed X times. Let Y be the number of
Heads and Z be the number of Tails. Find the joint and marginal distributions
of Y and Z.
). After observing X a coin landing
Heads with probability p is tossed X times. Let Y be the number of
Heads and Z be the number of Tails. Find the joint and marginal distributions
of Y and Z.
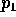 be the bivariate normal density with mean 0,
unit variances and correlation
be the bivariate normal density with mean 0,
unit variances and correlation 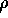 and let
and let 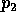 be the standard
bivariate normal density. Let
be the standard
bivariate normal density. Let 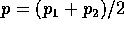 .
Show that p has normal margins but is not bivariate normal.
.
Show that p has normal margins but is not bivariate normal.
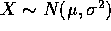 and
and 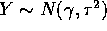 . Let Z=X+Y.
Find the distribution of Z given X and that of X given Z.
. Let Z=X+Y.
Find the distribution of Z given X and that of X given Z.
SET C
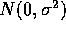 .
.
- Show that
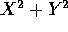 and
and 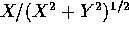 are independent.
are independent.
- Show that
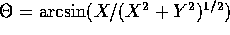 is uniformly
distributed on
is uniformly
distributed on 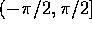 .
.
- Show
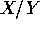 is a Cauchy random variable.
is a Cauchy random variable.
SET E
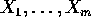 are iid
are iid 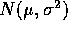 and
and
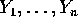 are iid
are iid 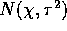 .
.
- Find complete and sufficient statistics.
- Find UMVUE's of
 and
and 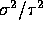 .
.
- Now suppose you know that
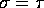 . Find UMVUE's of
. Find UMVUE's of
 and of
and of 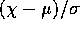 . (You have already found
the UMVUE for
. (You have already found
the UMVUE for 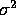 .)
.)
- Now suppose
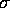 and
and  are unknown but that you
know that
are unknown but that you
know that 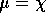 . Prove there is no UMVUE for
. Prove there is no UMVUE for 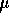 .
(Hint: Find the UMVUE if you knew
.
(Hint: Find the UMVUE if you knew 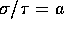 with a known.
Use the fact that the solution depends on a to finish the proof.)
with a known.
Use the fact that the solution depends on a to finish the proof.)
- Why doesn't the Lehmann-Scheffé theorem apply?
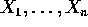 iid Poisson(
iid Poisson( 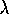 ). Find the
UMVUE for
). Find the
UMVUE for 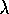 and for
and for 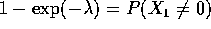 .
.
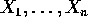 iid with
iid with
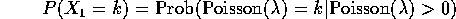
for 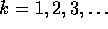 . For n=1 and 2
find the UMVUE of
. For n=1 and 2
find the UMVUE of 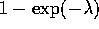 .
(Hint: The expected value of any function of X is a power series in
.
(Hint: The expected value of any function of X is a power series in
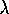 divided by
divided by 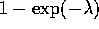 . Set this equal to
. Set this equal to
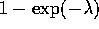 and deduce that two power series
are equal. Since this implies their coefficients are the same you can see what
the estimate must be. )
and deduce that two power series
are equal. Since this implies their coefficients are the same you can see what
the estimate must be. )
SET F
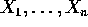 are independent Poisson(
are independent Poisson(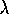 )
variables. Find the UMP level
)
variables. Find the UMP level  test of
test of 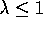 versus
versus 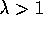 and evaluate the constants for the case n=3 and
and evaluate the constants for the case n=3 and
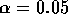 .
.
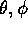 ) distribution with shape
parameter
) distribution with shape
parameter 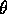 known. Find the UMPU test of
known. Find the UMPU test of 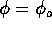 and
evaluate the constants for the case
and
evaluate the constants for the case 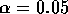 and
and 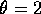 .
.
SET G
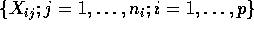 are independent
are independent
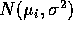 random variables. (This is the
usual set-up for the one-way layout.)
random variables. (This is the
usual set-up for the one-way layout.)
- Find the MLE's for
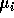 and
and 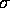 .
.
- Find the expectations and variances of these estimators.
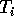 be the error sum of squares in the ith cell in the
previous question.
be the error sum of squares in the ith cell in the
previous question.
- Find the joint density of the
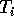 .
.
- Find the best estimate of
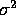 of the form
of the form 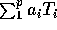 in the sense of mean squared error.
in the sense of mean squared error.
- Do the same under the condition that the estimator must be unbiased.
- If only
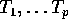 are observed what is the MLE of
are observed what is the MLE of 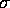 ?
?
- Find the UMVUE of
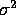 for the usual one-way layout model,
that is, the model of the last two questions.
for the usual one-way layout model,
that is, the model of the last two questions.
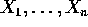 are iid with density
are iid with density
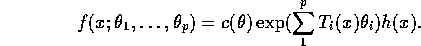
- Find minimal sufficient statistics.
- If
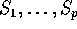 are the minimal sufficient statistics show
that setting
are the minimal sufficient statistics show
that setting 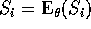 and solving gives the
likelihood equations. (Note the connection to the method of moments.)
and solving gives the
likelihood equations. (Note the connection to the method of moments.)
SET H
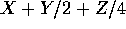 at 1. You may use the splus function
integ.romb (or any other function) found by attaching the directory
at 1. You may use the splus function
integ.romb (or any other function) found by attaching the directory
/home/math/lockhart/research/software/quadrature/.Data.
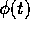 be
the characteristic function of X. Show that
be
the characteristic function of X. Show that
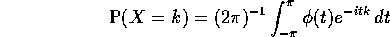
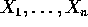 are independent random variables such that
are independent random variables such that
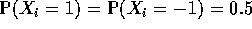 . Prove that
. Prove that
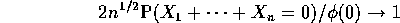
where 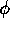 is the standard normal density. You should use the previous
problem and Taylor expansion of the characteristic function around 0.
Also do the same thing using Sterling's formula.
is the standard normal density. You should use the previous
problem and Taylor expansion of the characteristic function around 0.
Also do the same thing using Sterling's formula.
SET I
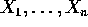 are iid exponential(
are iid exponential(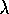 ).
).
- Find the exact confidence levels of 95% intervals based on normal
approximations to the distributions of the pivots
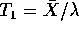 ,
, 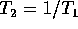 , and
, and 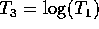 for n=10, 20 and 40.
for n=10, 20 and 40.
- Find the shortest exact 95% confidence interval based on
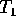 ; get numerical values for n=10, 20 and 40.
; get numerical values for n=10, 20 and 40.
- Find the exact confidence level of 95% confidence intervals based
on the chi-squared approximation to the distribution of deviance drop.
Compare the results with the previous question based on length and
coverage probabilities.
Figure out how to make a convincing comparison. Which method is better?
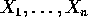 are iid with density f. Assume the median
of f is 0. In this problem you will study the asymptotic distribution of
the sample median. To simplify things you may assume that n=2m-1 is odd
so that the median is the mth order statistic.
are iid with density f. Assume the median
of f is 0. In this problem you will study the asymptotic distribution of
the sample median. To simplify things you may assume that n=2m-1 is odd
so that the median is the mth order statistic.
- Let M denote the sample median and
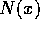 be the number of X's
less than or equal to x. Express the event that
be the number of X's
less than or equal to x. Express the event that 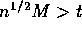 in terms of the number
in terms of the number 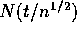 .
.
- What is the exact distribution of
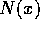 ?
?
- Show that the expected value,
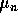 , of
, of 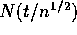 can be
written as
can be
written as 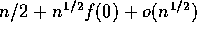 .
.
- Show that
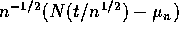 is asymptotically normal
with mean 0 and variance
is asymptotically normal
with mean 0 and variance 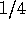 .
.
- Deduce from all the preceding that
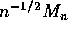 is asymptotically
normal with mean 0 and variance
is asymptotically
normal with mean 0 and variance 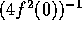 .
.
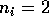 for all i and let
for all i and let 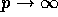 . What happens to
the MLE of
. What happens to
the MLE of 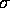 ?
?
SET J
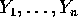 are independent random variables
and that
are independent random variables
and that  are the corresponding values of some covariate.
Suppose that the density of
are the corresponding values of some covariate.
Suppose that the density of 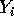 is
is
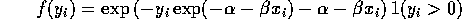
where  , and
, and 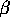 are unknown parameters.
are unknown parameters.
- Find the log-likelihood, the score function and the Fisher information.
- For the data set in /home/math/lockhart/teaching/801/data1 fit the
model and produce a contour plot of the log-likelihood surface, the profile
likelihood for
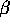 and an approximate 95% confidence interval for
and an approximate 95% confidence interval for
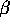 .
.
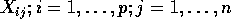 and a model
and a model 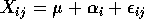 where the
where the  's are iid
's are iid 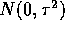 and the
and the  's are iid
's are iid 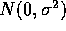 .
.
- Write down the likelihood.
- Find minimal sufficient statistics.
- Are they complete?
- Find method of moments estimates of the three parameters.
- Can you find the MLE's?
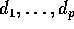 a number of animals
a number of animals 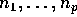 are treated with the corresponding dose of some drug. The
number dying at dose d is Binomial with parameter
are treated with the corresponding dose of some drug. The
number dying at dose d is Binomial with parameter 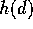 . A common model
for
. A common model
for 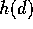 is
is 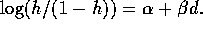
- Find the likelihood equations for estimating
 and
and 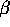 .
.
- Find the Fisher information matrix.
- Define the parameter LD50 as the value of d for which
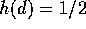 ;
express LD50 as a function of
;
express LD50 as a function of  and
and 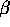 .
.
- Use a Taylor expansion to find large sample confidence limits for LD50.
- At each of the doses -3.204, -2.903, 2.602, -2.301 and -2.000 a sample
of 40 mice were exposed to antipneumonococcus serum. The numbers surviving
were 7, 18, 32, 35, and 38 respectively. Get numerical values for the theory
above. You can use glm or get preliminary estimates based on linear
regression of the MLE of
 against dose.
against dose.
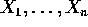 are a sample of size n from the density
are a sample of size n from the density
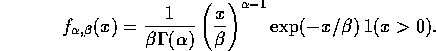
In the following question
the digamma function 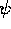 is defined by
is defined by
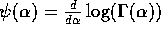 and the trigamma
function
and the trigamma
function 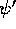 is the derivative of the digamma function. From
the identity
is the derivative of the digamma function. From
the identity 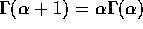 you can deduce
recurrence relations for the digamma and trigamma functions.
you can deduce
recurrence relations for the digamma and trigamma functions.
- For
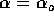 known find the mle for
known find the mle for 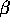 .
.
- When both
 and
and 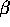 are unknown what equation must be
solved to find
are unknown what equation must be
solved to find 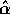 , the mle of
, the mle of  ?
?
- Evaluate the Fisher information matrix.
- A sample of size 20 is in the file
/home/math/lockhart/teaching/801/gamma.
Use this data in the following questions. First take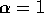 and find
the mle of
and find
the mle of 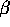 subject to this restriction.
subject to this restriction.
- Now use
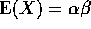 and
and 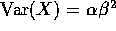 to
get method of moments estimates
to
get method of moments estimates 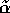 and
and 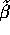 for
the parameters.
for
the parameters.
- Do two steps of Newton Raphson to get MLEs.
- Use Fisher's scoring idea to redo the previous question.
- Compute standard errors for the MLEs and compare the difference
between the estimates in the previous 2 questions to the SEs.
- Do a likelihood ratio test of
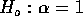 .
.
SET K
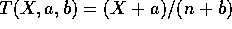 for b > 0.
for b > 0.
- Find the risk functions for these estimators.
- For the Beta
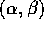 prior distribution on p
with
prior distribution on p
with  and
and 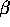 both positive find the posterior
distribution of p given X.
both positive find the posterior
distribution of p given X.
- Find the Bayes procedures for these priors.
- Discuss consistency and asymptotic distribution theory for the Bayes
procedures.
- Find the minimax procedure.
- Compare the risk function of the minimax procedure, the MLE and the
estimate
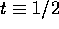 for n=1,100 and asymptotically. Provide
graphs.
for n=1,100 and asymptotically. Provide
graphs.
- What happens to the posterior distribution of p as n tends to
infinity?