Introduction to Solid-state NMR.

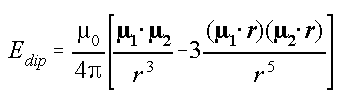
    NMR of solids is very different from that of liquids, for a simple reason: in liquids the molecules move, in solids they do not (usually). There are several important interactions which are not seen in liquids because molecular motion causes their average value to become zero. In solids no averaging occurs, and the interaction is seen.

    For spin ½ nuclei, which are the only ones considered here, the most important such interaction is the direct magnetic interaction between pairs of spins. (This is the direct through-space interaction between pairs of magnetic dipoles, not the J-coupling seen in liquids, which operates through chemical bonds). The energy of interaction between a pair of magnetic dipoles is given by

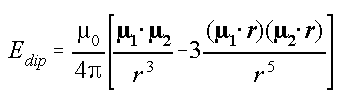
(Most NMR textbooks quote this without explanation or derivation. A derivation for the case of electric dipoles is given in reference (1). The magnetic result is the same apart from different units.)

    This interaction energy is traditionally turned into a quantum-mechanical operator by replacing the magnetic dipole vector µ_i with Î_i where , the gyromagnetic ratio, is a property of the nucleus, and Î is the nuclear spin operator. The vector r is then expressed in Cartesian coordinates, and E_dip is decomposed into a sum of terms involving various spin operators and angular functions. (For this decomposition, see reference 2, 3 or 4.) In the case that the two spins are nuclei of different types, the first-order splitting of the resonance by the dipolar coupling is given by D(3 cos² - 1) where D = (µ₀/4)(/2)₁₂/r³. In these equations r is the distance between the pair of interacting spins, and is the angle between the line joining the spins and the direction of the magnetic field. (If the spins are identical, the splitting turns out to be of the same form but 1.5 times larger)

    From the above, we can see that if we have a single crystal containing isolated pairs of spins, the spectrum would be a pair of lines with a separation of order of magnitude D, and this separation would depend on the orientation of the crystal in the magnetic field, because of the term in . Some crystals, such as CaSO₄.H₂O approximate to this situation: the effect of the r^-3 term is to make the coupling of the two protons in a single H₂O molecule much larger than couplings to distant protons. In such crystals, the expected "Pake doublet" is seen. For proton pairs at chemical distances, D is of the order of a few 10's of kHz. All other stable nuclei have a smaller than do protons, and typically longer bond lengths, leading to weaker dipolar couplings.

    If we have not a single crystal, but a solid powder, all values of will be present for different crystallites, and the spectrum will be a superposition of Pake doublets corresponding to all possible values of . Note that (3 cos² - 1) can take on all values from -1 to +2. The result of this is that each line of the doublet becomes a powder pattern extending over the whole range of frequencies permitted by the variation of (3 cos² - 1). The shape of these patterns is an inverse square root function, as shown in the diagram below. The separation of the peaks is D in the heteronuclear case, and 1.5D for a homonuclear spin pair.

    Powder patterns approximating to the above are found for solids, like CaSO₄.H₂O that contain approximately isolated spin pairs.

    Note that dipolar coupling usually plays no role in liquid NMR spectra, because if molecular motion allows inter-spin vectors to randomly take all orientations in space, the average value of (3 cos² - 1) is zero. (Consider that the vector starts at the origin and terminates in an area element dA on the surface of a sphere. For random distribution of vectors, the probability of this orientation is dA/4r², and since dA = r² sin dd,  <(3 cos² - 1)> will be proportional to  (3 cos² - 1) sin d from 0 to , which is equal to 0).

    While the spectrum of dipolar-coupled spin pairs is simple, that of a solid containing many spins of approximately equal couplings is not. Generally a featureless blob is all that is seen. There is no known solution for the exact shape of such lines, even for spins positioned on a simple 3-dimensional lattice. Experimentally, the line shapes are often close to Gaussian. Interestingly, there is an exact formula for the second moment of the line shape. If f() is the line shape function, and the centre of the line is at ₀, the second moment, M₂ is defined by

As shown in references 3 and 4, M₂ is proportional to the average value of r^-6 in the sample, so an experimental determination of M₂ allows the average spacing of the spins to be determined. Reference 3 describes the classic experiment of Andrew and Eades which determined the CH bond length in benzene from measurement of M₂.

    For most purposes dipolar coupling is not helpful, and one would like to avoid it so as to observe chemical shifts and other phenomena which are only visible when lines are narrow. There are four methods by which this can be accomplished:

1.	Use a magnetically dilute sample. The first high-resolution solid spectrum was obtained this way (5) in a study of the 13C spectrum of CaCO3. The only magnetic species are 13C, 17O and 43Ca, whose abundances are 1.1%, 0.04% and 0.15% respectively. So, on average a given 13C is far away from other spins, and the r-3 term makes the dipole interaction small. A line width of about 8 Hz was observed in this study.
2.	Combine dilution with decoupling. There are few solids in which all inter-spin distances are large. It is often the case however (e.g. many organic solids) that there is a dilute spin (13C) and a chemically different abundant spin (1H). By strongly irradiating the abundant spin, its effects on the dilute spin can be decoupled, and narrow lines can be obtained for the dilute spin (typically 13C, 15N, 29Si, etc.). This is the same concept as heteronuclear decoupling in liquid NMR, but the decoupling field required is an order of magnitude larger, which requires careful probe design.
3.	Magic angle spinning (MAS). <(3 cos2 - 1)> = 0 in a liquid, due to random molecular motions. Can we impose a motion on a solid which will have the same effect? Yes. The function (3 cos2 - 1) is equal to 0 for  = 54.7°, the so-called magic angle. If the sample is spun rapidly about an axis which makes this angle with the applied magnetic field, B0, <(3 cos2 - 1)> is again zero. In this diagram the line XY makes an angle of 54.7° with B0. If a spin A at the origin is oriented along B0, parallel spins in the yellow region interact attractively, whereas those in the white region interact repulsively. Thus the dipolar interaction between spins A and B is repulsive. If the sample is rotated about XY, the spin at B moves to C after a half rotation, and the interaction is now attractive. After a complete revolution the spin returns to the repulsive position B. It can be shown (for example in Appendix 5 of reference (2)) that the average of (3 cos2 - 1) is zero over the complete rotation.     This rotation removes the effect of dipolar interaction from the spectrum if you can do it fast enough. This means the spinning speed must be greater than the dipolar coupling expressed in Hz. This can be rather demanding. It is fairly easy to spin samples at a few kHz, and faster speeds are progressively more difficult due to problems with balance and strength of materials. The fastest commercially-available spinners achieve speeds around 20 kHz, on very small samples. This is fast enough to remove all interactions except those with H or F at chemical-bond distances. The combination of decoupling (of H or F if present) with MAS makes possible high-resolution spectra of all spin ½ nuclei except 1H and 19F.
4.	Multiple-pulse line narrowing. The above methods do not permit high-resolution spectroscopy in the presence of strong H-H or F-F dipolar interactions. The most satisfactory way of doing this is with multiple-pulse experiments. These manipulate the spins by a continuous cyclic sequence of r.f. pulses such that the dipolar coupling of like nuclei averages to zero over a cycle (of typically 8 pulses). These methods are described in references 3 and 6. These techniques are also difficult, and it is unusual to achieve proton line widths less than about 0.5-1 ppm, rather unsatisfactory in comparison with liquid NMR.

    Once we have suppressed the dipolar interaction, we learn something new: chemical shifts are anisotropic - that is, they depend on the orientation of the molecule in the magnetic field. This manifests itself in single-crystal spectra as lines whose position varies when the crystal is rotated. In powdered samples, a powder pattern is again seen, whose shape can be different from that of a dipolar powder pattern.

    Chemical shift is not a number, as commonly assumed in liquid NMR, it is a second-rank tensor property. (For a short introduction, see Appendix 4 of ref. (2), for more, see ref. (7)). To first order, the chemical shift tensor appears symmetric, and can be thought of as represented by a symmetric 3x3 matrix. The field at the nucleus is given by B_nuc = B₀ + B_cs where vector B₀ is the applied magnetic field, and B_cs is the chemical shift field arising from perturbations of the electron motions. B_cs = [ S] B₀ where S is the chemical shift tensor. This problem looks simple in a coordinate system where the off-diagonal elements of S are zero. The coordinate axes in this system are called the principal axes of S. The non-zero diagonal elements often have the symbols _xx, _yy and _zz and characterize the size of the chemical shift. The orientation of the principal axes within the molecule is often determined by symmetry (7).

    The observed chemical shift for a molecule is given by

where and are the polar angles of B₀ with respect to the principal axes of S. This expression gives the shift that would be observed as a function of angle in a single crystal experiment. For a molecule in a liquid, the angular functions are changing continuously due to molecular rotation, and we need to consider their average values. As shown in (2), for an isotropic rotation, each of the above angular functions has an average value of 1/3. So in a liquid we see _liq = (_xx + _yy + _zz)/3. In a powdered solid we see a powder pattern whose appearance depends on the values of _xx, _yy and _zz. If these values are all equal, it follows from the identity cos²x + sin²x = 1 that _obs is independent of angle, so all crystallites resonate at the same shift, and a single narrow line is seen. This situation is required by symmetry when the observed nucleus lies on a site of tetrahedral or higher symmetry.

    If the nucleus lies on an axis of 3-fold or higher symmetry, one of the principal axes must coincide with the symmetry axis, and the components of S perpendicular to the axis must be equal. In this situation S is said to be "axially symmetric", and the components parallel and perpendicular to the axis are often denoted as _|| and respectively. In this case, taking the symmetry axis to lie along z, the above equation becomes _obs = _||  cos² +   sin² = _av + (3 cos² - 1)/3 where _av = (2  +  _|| )/3 and  = (_||  - ). This has the same angular dependence as the dipolar splitting, and consequently the same shape of powder pattern (inverse square root) arises, with the singularity at .
   

If neither of the above symmetry conditions applies, all of the principal values are different, and the powder pattern looks something like this,

where the corners are located at the highest and lowest principal values, and the singularity at the intermediate one.

    It is obvious from the treatment above for the axially symmetric case that MAS will make the angular dependence (3 cos² - 1) vanish on average, and the powder pattern will collapse to a single line at _av, the same value as observed in a liquid. The same result is obtained in the general case, as shown in (2).

    To summarize, there are three kinds of chemical shift measurements that can be done in a solid. Magic angle spinning produces a sharp line at the same average shift as is observed in a liquid, to which it can be directly compared. Observation of a static powder produces a powder pattern, from which the three principal values of the chemical shift can be obtained. (They can also be obtained from the spinning sidebands which appear in a MAS spectrum when the spinning rate is not high enough). Finally experiments on a single crystal will produce sharp lines whose position will change as the crystal is rotated. By observation at a large number of orientations it is possible to determine both the principal values of the chemical shift, and the orientation of the principal axes within the molecule.

    In general solid-state NMR may produce more lines than you might have expected from the liquid spectrum. There may be less symmetry than in the liquid, because internal rotations are locked in the crystal. A well-known example is alkoxy aromatics, such as

In the liquid phase this shows two ¹³C lines from the ring carbons, because free rotation about the ring-O bonds makes the two sides of the ring equivalent. In the solid the molecule is frozen in the conformation shown, and three ring carbon lines are seen. In general MAS NMR on a solid will produce a line from each atom in the crystallographic asymmetric unit.

    Another situation can arise with single crystal spectra; atoms which are chemically identical can become magnetically different based on the orientation of the magnetic field. In the following diagram,

two molecules (solid arrows) are related by a crystallographic mirror plane (dashed line). Because of this symmetry element, the molecules are chemically identical, and using MAS, which averages out all angular dependencies, their spectra will be identical. However, if we have a single crystal, we might position it so that the magnetic field points in the direction of the dotted line. Now assume that one of the principal directions points along the arrow. For one molecule the field is nearly perpendicular to this principal direction, while for the other it is nearly parallel. The result is that and will be different for the two molecules and their atoms will show separate resonances. In general a single crystal that lacks an inversion centre will show a line for every atom in the primitive unit cell. If inversion symmetry is present, atoms related by inversion have the same resonance frequency in all orientations.

References:

1.	N. A. Anderson, The Electromagnetic Field, Plenum, New York, 1968.
2.	R. K. Harris, NMR Spectroscopy, A Physicochemical View, Longman, Burnt Mill, 1986.
3.	C. P. Slichter, Principles of Magnetic Resonance, Springer, Berlin, 1990.
4.	A. Abragam, The Principles of Nuclear Magnetism, O.U.P., London, 1961.
5.	P. Lauterbur, Phys. Rev. Lett. 1,343 (1958).
6.	B. C. Gerstein and C. R. Dybowski, Transient Techniques in NMR of Solids, Academic Press, Orlando, 1985.
7.	J. F. Nye, Physical properties of crystals, their representation by tensors and matrices, Clarendon Press, Oxford, 1964.

© Ian D. Gay, 1999. Individuals may make single copies of this page for personal study. Mass duplication is prohibited. Maintainers of web sites may link to this page, but may not copy it onto other computers without my permission. e-mail: