Delta Notation
When I ask you what time it is, I am really asking you to give me a clock reading. However, when I inquire how much time some event takes, I want to know an interval of time. These are two senses in which we use time. In physics we generally mean a time interval instead of a clock reading. In fact, the time on the clock is really the interval of time from midnight last night. To distinguish mathematically between an interval and a clock reading we use what is known as "Delta Notation". Let us consider two clock readings, for example the readings at the beginning and ending of a race. Use the letter t with subscripts 1 and 2 to designate the first and second reading respectively. The time interval is indicated by writing a big Greek delta, Δ, before the t like this:
Δ t = t2 − t1 The Δ does not mean "multiplied by Δ". It is just a prefix indicating a change in the quantity t. For the mundane events that we shall be discussing, time always goes forward and Δt is always positive.
The delta notation can be used for any quantity that changes. In particular, position can change. And, unlike time, it can change both ways so Δx can be either positive or negative.
A Frame of Reference
In order to be able to talk about the position of something we must establish a coordinate system, a.k.a., frame of reference. Let's confine ourselves to describing something moving back and forth along one line. We'll have enough trouble in one dimension before we advance to two and three dimensional movement.
Displacement
The position of an object is where it sits on the number line. When the object moves to another position, its displacement is the second position minus the first position.
Δ x = x2 − x1 The word displacement implies we keep track of which way the movement occurs. In one dimension the direction is indicated by the sign: negative if to the left and positive if to the right. The word distance means how far the object moves regardless of direction. It is always positive and is equal to the absolute value, or magnitude, of the displacement.
If one follows the rule of always subtracting the first position from the second, the sign always works out to be positive if the displacement is to the right and negative if the displacement is to the left. (This assumes the frame of reference with the positive side of the axis on the right). When we illustrate the displacement by drawing an arrow with its tail at the first position and the tip of its arrow at the second, it will point to the right for positive displacement and to the left for negative displacement.
When displacements occur on the negative side of the axis, it's easy to make a mistake with double minus signs. When you calculate displacements you should first draw the arrow, then calculate the value and finally check that the sign agrees with the direction of the arrow.
Displacement and Distance, What's the Difference?
We have defined displacement very precisely. In this definition the sign is very important. A journey from the position +3 to −3 is a displacement of −6 m. The return trip from −3 to +3 is +6 m displacement. The total displacement for that trip is got by adding the two displacements: (−6 m) + (+6 m) = 0 m. The total distance travelled in the entire trip is not zero, it is 12 m.Thus the words distance and displacement have very different meanings as we use them in physics.
Some small jaunts
Here are several examples of displacements:
Here we have a positive displacement taking place on the positive side of the axis. The start and finish are on the positive side of the axis, the starting position is smaller than the finish. Therefore, the displacement is positive.
When the finish is closer to the origin and both are on the positive side of the axis then the displacement is negative. The arrow points to the left, the displacement is negative and all is right with the world.
Displacement towards the origin on the negative side of the axis is positive. Subtracting −4 from −1 gives a positive +3. The arrow points to the right so the sign is right.
Going to the left should give a negative displacement even on the negative side of the origin. Subtracting −2.5 from −4 leaves −1.5. Good!
Calculating displacements which cross the origin can be tricky. But the direction of the arrow never fails to give the correct sign. Here are the last two examples.
The sign of the displacement does not depend on where the displacement takes place, but only on its direction. In fact, if the number line had been displaced left or right, all the position measurements would be different, but the displacements wouldn't change.
Graphs of position vs time
Motion that takes place back and forth along the number line can be represented by a position-time graph. The horizontal dimension of the graph represents time, with time flowing from left to right. The number line is represented by the vertical dimension of the graph with positive positions above the time axis and negative positions below it.
Take a little trip...
Let's take a trip and show what it would look like on a position-time graph. I ride a Ninja Kawasaki Power-Wheels which has two forward speeds and one reverse. I start out from the −5 position in high, then shift to low and, after a few seconds, screech to a stop. Throwing it into reverse, I back up to about the origin, stop and get off. Here's what a graphical representation of that trip might look like.
During the first two seconds, I accelerate to the high velocity. Velocity is defined as the change in position divided by the time interval during which that change occurred:
According to the graph, the velocity is pretty constant from the second to the fourth second. Between 2.5 s and 3.5 s Δx is about 2.57 m. Δt is 1 s. Thus v = 2.57m/1s = 2.57 m/s in the high-speed region. 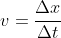
The word speed is usually used to indicate the absolute value of the velocity. Velocity can be negative when its going towards the negative side of the axis. Speed will be positive in that case. In other words, speed is distance travelled divided by the time interval.
[ The distinction between speed and velocity, and distance and displacement is a useful one, but the words used are arbitrary. I will try to use these words consistently as I have defined them in these lectures. You should note though, that sometimes other authors may not be quite so consistent. In particular the first edition of PSSC Physics in our library uses speed, in the one-dimensional case, to mean displacement divided by time interval, that is, our velocity. The second and later editions use the term the same way that we do.]
After pushing the low-speed button, the cart slows down or decelerates. We use the word "acceleration" for this slowing down too. When the cart is moving in the positive direction, slowing down will technically be called acceleration which is negative. Between t = 5.5 s and t = 8.5 s the velocity is relatively constant. As you can see, during a 1 s interval in this region, the cart covered 0.85 s. Thus the velocity here is 0.85 m/s.As it comes to a stop, the cart again negatively accelerates. In other words, the cart looses some of its positive velocity until it reaches zero. Zero velocity is a horizontal line on the graph.
As it starts to back up, the cart again has "negative acceleration" but now it is gaining speed in the negative direction. During the period of time when the speed is constant, going backward, the graph indicates a displacement of −0.85 m in one second.
Thus v = −0.85 m/s, negative velocity. This is the same speed as the forward low speed, but not the same velocity. Slowing down to a stop involves loosing negative velocity, which, mathematically, is called positive acceleration.Now this position-time graph was completely made up. I haven't yet measured the true motion of my cart. How are we going to do that?