Energy in Springs
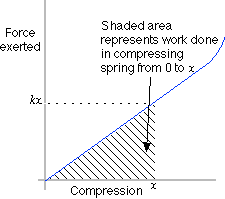
Springs are a common device for storing energy. A spring which is compressed from its by an amount x from its equlibrium length exerts a force
Force spring pushes on hand: F = –kx
In order to push a spring to a length shorter than its equlibriium length it is necessary to balance the spring’s force. Thus the pushing force must be
Force hand pushes on spring: F = kx
to keep the spring compressed by x. When the hand first started compressing the spring almost no force was needed. Thereafter the force gradually increases until the point x.
The area of the shaded triangle is the work done by the hand compressing the spring.
W =(1/2)k x2
Collision with a Spring Bumper
Think of a block moving right toward a spring bumper. Before the block hits the spring, it has a speed of 1 m/s. The block’s mass of 1 kg and the spring has a spring constant of 1 N/m.
We can calculate approximately what happens after the block starts to compress the spring in 2 cm intervals. During the first 2 cm the spring has very little force. The average force is that at 1 cm compression
F(1 cm) = (1 N/m)(0.1 m) = 0.1 N
The work done by the block during the first 2 cm is
Wavg(0.2cm) = (0.1 N)(0.2m) = 0.02 J
This work represents energy transferred to the spring and stored in it. The energy comes from the kinetic energy of the block which is slowing down. One can continue calculating the energy transferred from the block to the spring in 2 cm intervals until all the block's kinetic energy is used up and stored in the spring. That is when the block is stopped and the spring is compressed the most.
The approximation means that we calculate the work done in compressing the spring by the stair-stepped light blue area on the graph, rather than the area under the dark blue line. The total work done is (1/2) k x2 which, in this case, is the same as the stair-stepped area. It works out to 0.5 J of energy. At each step along the way the work done is taken from the moving object’s kinetic energy and transferred to kinetic energy in the spring. The following table shows the calculation step-by-step.
x (m)
F-avg (N)
W (J)
KE (J)
PE (J)
0.00 0.50 0.00 0.10 0.10 0.02 0.20 0.48 0.02 0.30 0.30 0.06 0.40 0.42 0.08 0.50 0.50 0.10 0.60 0.32 0.18 0.70 0.70 0.14 0.80 0.18 0.32 0.90 0.90 0.18 1.00 -0.00 0.50
The following illustration shows the object at each step during the calculation with a bar graph depicting the potential energy and kinetic energy of the system.

After the spring is fully compressed, it starts to expand, giving back its stored energy to the block which starts to go back from whence it came. If no energy is lost in the process, the block finally exits the bumper with the same speed as it came in with, but moving in the opposite direction. This reverse process is not depicted here, but you can sketch it out for yourself as an exercise.