Collisions





One can use the explosion of a spring between two carts (like you did in the lab) to measure the mass of an unknown object. Suppose that both carts have the same mass, m, which is known and that the unknown object has mass M. Thus the cart carrying the extra mass has total mass m+M.


Before the explosion, the total momentum is zero because neither cart is moving. After the collision the empty cart has velocity v1’. The cart carrying the extra mass will have velocity v2’. v1’ and v2’ will have opposite signs and v1’ will be larger. The total momentum after the collision must be zero:

p1’ + p2’ = mv1’ + (m+M)v2’ = 0

(m+M)v2’ = –mv1’

mv2’ +Mv2’ = –mv1’

Mv2’ = –mv1’– mv2’

M = (– mv1’– mv2’)/v2’

M = (– v1’/v2’–1)m

Because v2 and v1 are in opposite directions the ratio – v1’/v2’ is positive. Because cart 2 carries the extra mass, its speed will be slower and the ratio is greater than one.

For example if v1’ is –3 m/s, v2’ is 1 m/s and the cart has a mass of 0.5 kg, then the mass of the object is

M = [–(–3 m/s / 1 m/s) –1] 0.5 kg = 1 kg.

Hit and Stick: Inelastic Collision



A common event is the collision of a moving object with another object in which both of them stick together after the collision. Such collision is called “inelastic” because there is no bounce. Any collision in which kinetic energy is lost is inelastic. An elastic collision is one in which the kinetic energy after is the same as the kinetic energy before. If there is some “bounce” but the final kinetic energy is less than the initial kinetic energy then the collision is called inelastic. A collision in which the bounce is completely absent is sometimes called “completely” inelastic. Completly inelastic collisions which end by the objects sticking together loose the most kinetic energy. This situation is accomplished in the lab by Velcro™ pads on the cart ends.

Imagine the reverse of the explosion that we just discussed. Both carts come towards each other in a head-on collision. If both carts have the same masses and speeds then they will both come to rest after they hit the Velcro pads. This collision is completely inelastic: all the kinetic energy disappears. It is hardly necessary to do any mathematical analysis to understand the outcome.


Rear-end Collission


There is a devious trick used by professional physicists that I would like to show you. In the head-on inelastic collision, the result was almost obvious. What about a rear-end collision where a moving cart hits a nonmoving cart and sticks? What is the velocity of the two carts after they hit? The trick is to imagine that we are travelling along at 1/2 the velocity of the moving cart. From this point of view, the stationary cart is coming towards us at –v/2 and the the cart approaching from behind is moving at +v/2. In other words, changing to this frame of reference subtracts v/2 from every cart’s velocity. The accelerations and forces are the same in both frames of reference so long as they are moving at constant velocity.

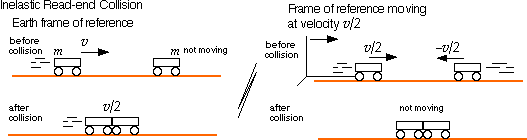
The result of the collision is obvious from the moving frame of reference: the carts will be stuck together and not moving. To find out how this looks to an observer on the ground just add v/2 to the velocity. The two carts end by moving at v/2 when viewed from the Earth’s frame of reference.


If changing frames of reference gives you a headache, then one can revert to a more pedestrian way of analysing the collision of the cart moving at velocity v with a stationary cart. The following analysis is more general in that the cars are allowed to have different masses, m1 and m2. At the end we can set the two masses equal and verify that the final result for identical carts is the same as we get by the above reasoning.

Initially the total momentum is

p1 + p2 = m1v + 0

After the collision the total momentum is the same as before,

mv1’ + mv2’ = 0.

In addition the two velocities are equal

v1’ = v2’ = v’.

p1’ +p2’ = (m1 + m2)v’.

Setting the initial and final momenta equal to each other allows predicting the final velocity:

m1v = (m1 + m2) v’

v’ = [m1/ (m1 + m2)] v.

If the two carts have the same mass then

v’ = v/2

Which is just the result that was predicted by jumping into and out of moving frames of reference.

Elastic Collisions: Hit and Bounce



In this case the bumpers have elastic bumpers which give back all the energy they absorb during the collision. The carts used in our lab exercise have magnets which oppose the magnets on the end of the colliding cart. These magnets act as almost perfectly elastic bumpers.

This type of collision can be analysed by assuming that both the total momentum and and the total kinetic energy are the same before and after the collision. An obvious case to analyse is that of two carts in a head-on collision. This time the elastic bumpers give back the energy, they don’t stick. It seems reasonable that after the collision, the two carts will have the same speeds by will be going in the opposite directions.



Elastic Rear-end Collision


One of the carts is not moving before it is hit the other cart is heading toward it at velocity v.
The following picture shows the situation. You are to follow the analysis in the say way that the inelastic rear-end collision was analysed by first moving to a frame-of-reference moving at v/2.
  1. Fill in the velocities of the two carts as it appears in the moving frame of reference. Use arrows to show direction. Hint: In this frame of reference, it is a head-on collision.
  2. Use what you know about elastic head-on collisions to sketch the situation after collision.
  3. Transform back to to the earth frame of reference and sketch the result of the collision.


We can now work out mathematically what happens in the earth frame of reference.
There is a mathematical trick which makes the analysis a little easier if we are willing to think in terms of momentum rather that velocity. The kinetic energy of a moving object is defined as (1/2)mv2. This can be expressed in terms of momentum as follows:

KE = (1/2) mv2
KE = (1/2m) m2v2
KE = p2/2m

The total momentum and kinetic energy is conserved from before to after the collision.

Before the collision we have
Total momentum : p1 + 0


Total Kinetic Energy: p12/2m1 + 0


After the collision

Total momentum: p1’ + p2’


Total Kinetic Energy: p1’2/2m1 + p2’2/2m2

Setting momentum before equal to momentum after and KE before equal to KE after gives two separate equations.

p1 = p1’ + p2’

p12/2m1 = p1’ 2/2m1 + p2’ 2/2m2

Transform the first equation by squaring both sides.
Transform the second by multiplying by 2m1.

p12 = p1’ 2 + 2 p1’p2’ + p2’ 2

p12 = p1’ 2 + (m1/m2) p2’ 2

subtract these two equations to give

(m1/m2) p2’2 = 2 p1’p2’ + p2’2

(m1/m2) p2’ = 2 p1’ + p2’

p1’ = (1/2) ( m1/m2–1 )p2’

This shows that when m1=m2, the first mass stops after the collision. This should be confirmed by the pictoral analsys above.


Using

p1 = p1’ + p2’

p1 = (1/2) (m1/m2 – 1) p2’ + p2’
p1 = (1/2)(m1/m2 +1) p2’

solving for p2’

p2’ = 2p1/(m1/m2 +1)

This gives the momentum of the second object as a function of the masses of the balls.
What happens if the second ball is very small compared to the first? Then (m1/m2+1)can be approximated by m1/m2

p2’ = 2p1/(m1/m2)


p2’/m2 = 2p1/m1

(m2 v2’)/m2 = 2 (m1 v1)/m1

v2’ = 2 v1.

The little runt takes off at twice the speed of the big guy.

(This is reasonable. Think of a ball hitting the ground with velocity –v and bouncing. After the bounce it is going +v and he change in velocity is 2v. Another way ot looking at this is that the ball is stationary an the earth comes up and hits it. According to our calculation the change in velocity is 2 v. The change in velocity is the same independent of the frame of reference.)

Solving for p1’

p1’ = p1 – p2’

= p1 – 2p1/(m1/m2) = p1(1– 2 m2/m1)

but if m1 >> m2 then p1’ is about p1, in other words, the original object is hardly affected by hitting the little runt.

The Basketball and the Tennisball



An impressive demonstration of the conservation of momentum and kinetic energy in an almost elastic collision occurs when a tennis ball is held on top of a basket ball several feet from the ground.Both are dropped. As they bounce, the basket ball rebounds from the floor and propells the tennis ball much higher than its initial height.

As the two balls fall together, they are essentally weightless, in free fall. Neither ball exerts a fther during the fall even though they stay together. The basketball is the first to hit the ground and reverse direction. Immedialely after reversing direction it hits the tennis ball which is still falling downwards. The collision of the more massive basketball with the tennis ball sends the tennis ball back up with a much larger velocity.

We can get an idea of the size of the gain in height by considerng the collisions to be perfectly elastic and considering the basket much more massive than then tennis ball so that the ration of the tenniss ball’s mass to that of the basket ball can be set to zero.


Move back to the earth frame of reference by adding v to all velocities. You can see that the tennis ball goes up at 3v while the basket ball continues up at slightly less than v. As the balls continue upward their kinetic energies are converted to potential energy until. The tennis ball has 3 times the velocity after the collision with the basket ball. Therefore, its kinetic energy is increased by a factor 9. Thus the total height that it can attain is 9 times more than that at which it was dropped. Of course the collision will not be completely elastic and the basketball’s mass is not infinite. The tennis ball will not quite reach 9 times its original height. Nevertheless the tennis ball’s flight is impressive.